For a cell, the terminal potential difference is 2.2V, when circuit is open and reduces to 1.8V. When cell is connected to a resistance R=5Ω, the internal resistance of cell (R) is
109Ω
910Ω
119Ω
59Ω
The correct Answer is:A
To find the internal resistance of the cell, we can follow these steps:
1. Identify Given Values:
- Open circuit terminal potential difference (V_open) = 2.2 V
- Terminal potential difference when connected to the resistance (V_load) = 1.8 V
- Resistance (R) = 5 Ω
2. Calculate the Current (I):
- When the cell is connected to the resistance, we can use Ohm's law to find the current flowing through the circuit.
- According to Ohm's law:
V=I×R
- Here, V is the potential difference across the resistor, which is 1.8 V. Thus:
1.8=I×5
- Rearranging gives:
I=1.85=0.36 A
3. Calculate the Potential Drop Across Internal Resistance (r):
- The potential drop across the internal resistance can be calculated as:
Vinternal=Vopen−Vload
- Substituting the values:
Vinternal=2.2−1.8=0.4 V
4. Use Ohm's Law to Find Internal Resistance (r):
- The potential drop across the internal resistance is given by:
Vinternal=I×r
- Substituting the known values:
0.4=0.36×r
- Rearranging gives:
r=0.40.36≈1.11 Ω
5. Conclusion:
- The internal resistance of the cell is approximately 1.11 Ω.
- Open circuit terminal potential difference (V_open) = 2.2 V
- Terminal potential difference when connected to the resistance (V_load) = 1.8 V
- Resistance (R) = 5 Ω
- When the cell is connected to the resistance, we can use Ohm's law to find the current flowing through the circuit.
- According to Ohm's law:
V=I×R
- Here, V is the potential difference across the resistor, which is 1.8 V. Thus:
1.8=I×5
- Rearranging gives:
I=1.85=0.36 A
- The potential drop across the internal resistance can be calculated as:
Vinternal=Vopen−Vload
- Substituting the values:
Vinternal=2.2−1.8=0.4 V
- The potential drop across the internal resistance is given by:
Vinternal=I×r
- Substituting the known values:
0.4=0.36×r
- Rearranging gives:
r=0.40.36≈1.11 Ω
- The internal resistance of the cell is approximately 1.11 Ω.
Similar Questions
The poten tial difference between the terminals of a cells is found to be 3 volts when it is connected to a resistance equal to its internal resistance. The e.m.f. of the cell is:-
View SolutionWhen current supplied by a cell to a circuit is 0.3A, its terminal potential difference is 0.9 A. When the current supplied becomes 0.2 A, its terminal potential difference becomes 1.0 V . The internal resistance of the cell is
View SolutionThe terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
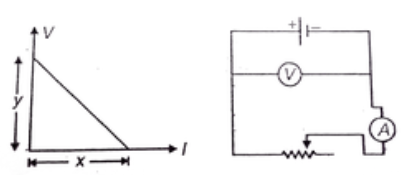
View SolutionFor a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn the cell. The emf and the internal resistance of the cell are E and r, respectively. Then
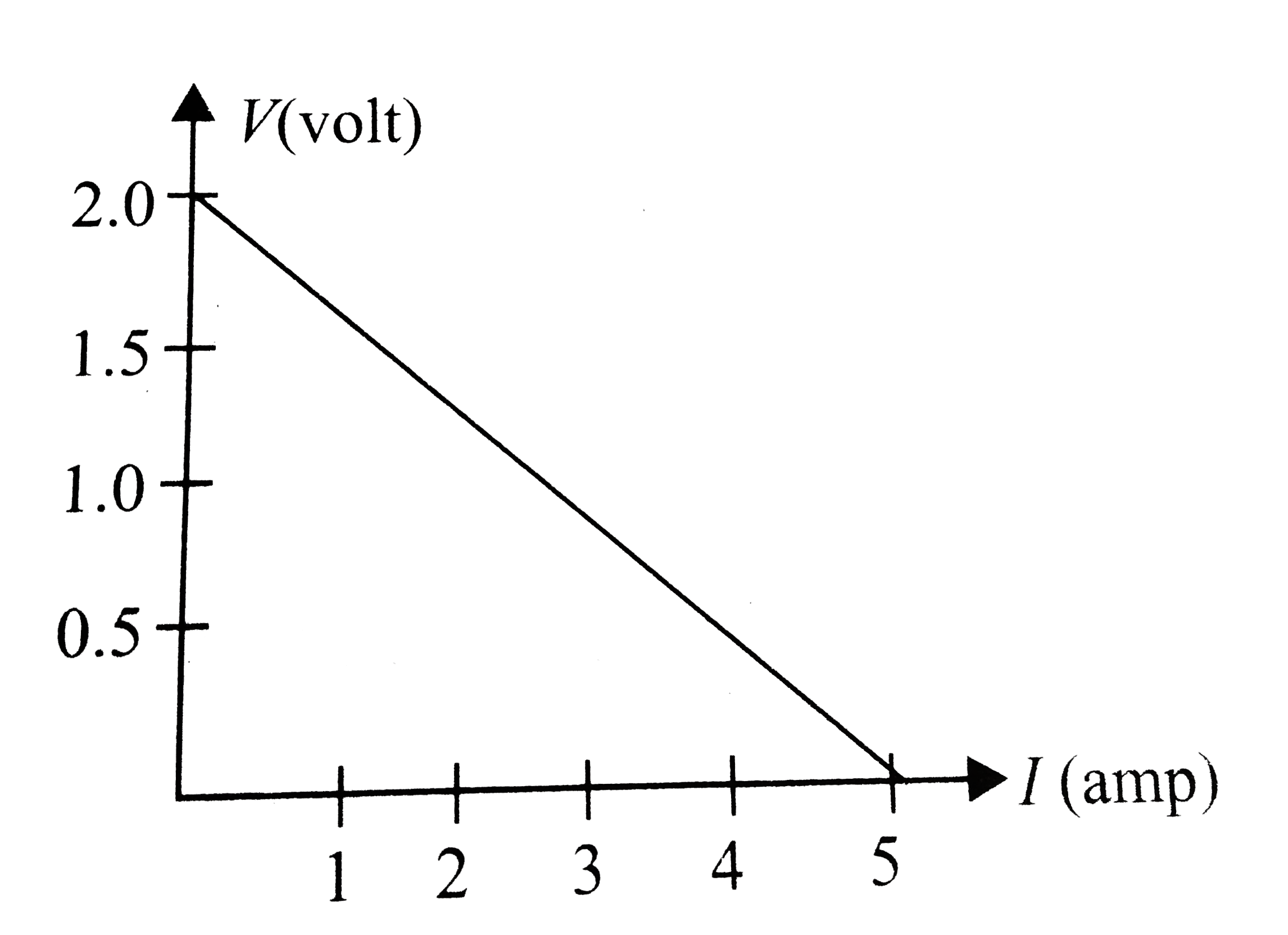
View Solution

