A manufacturer of clectronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is 50 and that on type B circuit is 60, formulate this problem as a LPP do that the manufacturer can maximise his profit. How many of circuits of Type A and of type B, should be produced by the manufacturer so as to maximise his profit? Determine the maximum profit.
The correct Answer is:Type -A : 6 units
Type -B : 3 units
Maximum profit = रु 480
To solve the problem, we will formulate it as a Linear Programming Problem (LPP) and then find the optimal solution to maximize profit.
Step 1: Define the Variables
Let:
- x = number of Type A circuits produced
- y = number of Type B circuits produced
Step 2: Formulate the Objective Function
The profit from Type A circuits is 50 per unit and from Type B circuits is 60 per unit. Therefore, the objective function to maximize profit Z is:
Z=50x+60y
Step 3: Formulate the Constraints
We have the following constraints based on the availability of resistors, transistors, and capacitors:
1. Resistors Constraint:
Each Type A circuit requires 20 resistors and each Type B circuit requires 10 resistors. The total available resistors are 200. Thus, the constraint is:
20x+10y≤200
Simplifying this gives:
2x+y≤20(Constraint 1)
2. Transistors Constraint:
Each Type A circuit requires 10 transistors and each Type B circuit requires 20 transistors. The total available transistors are 120. Thus, the constraint is:
10x+20y≤120
Simplifying this gives:
x+2y≤12(Constraint 2)
3. Capacitors Constraint:
Each Type A circuit requires 10 capacitors and each Type B circuit requires 30 capacitors. The total available capacitors are 150. Thus, the constraint is:
10x+30y≤150
Simplifying this gives:
x+3y≤15(Constraint 3)
Step 4: Non-negativity Constraints
Since the number of circuits produced cannot be negative, we have:
x≥0,y≥0
Step 5: Summary of the LPP
Maximize:
Z=50x+60y
Subject to:
2x+y≤20(Constraint 1)x+2y≤12(Constraint 2)x+3y≤15(Constraint 3)x≥0y≥0
Step 6: Finding the Corner Points
To find the corner points of the feasible region, we will solve the equations formed by the constraints:
1. Intersection of Constraint 1 and Constraint 2:
2x+y=20(1)
x+2y=12(2)
Solving these simultaneously gives (8,4).
2. Intersection of Constraint 2 and Constraint 3:
x+2y=12(2)
x+3y=15(3)
Solving these simultaneously gives (10.5,1.5).
3. Intersection of Constraint 1 and Constraint 3:
2x+y=20(1)
x+3y=15(3)
Solving these simultaneously gives (0,20).
4. Intercepts:
- For x=0 in Constraint 1: y=20
- For y=0 in Constraint 1: x=10
- For x=0 in Constraint 2: y=6
- For y=0 in Constraint 2: x=12
- For x=0 in Constraint 3: y=5
- For y=0 in Constraint 3: x=15
Step 7: Evaluate the Objective Function at Corner Points
Now we will evaluate Z=50x+60y at the corner points:
1. (0,20): Z=50(0)+60(20)=1200
2. (8,4): Z=50(8)+60(4)=400+240=640
3. (10.5,1.5): Z=50(10.5)+60(1.5)=525+90=615
4. (15,0): Z=50(15)+60(0)=750
Step 8: Determine the Maximum Profit
The maximum profit occurs at the point (15,0) with:
Maximum Profit=750
Conclusion
To maximize profit, the manufacturer should produce:
- 15 circuits of Type A and 0 circuits of Type B.
- The maximum profit will be 750.
Let:
- x = number of Type A circuits produced
- y = number of Type B circuits produced
The profit from Type A circuits is 50 per unit and from Type B circuits is 60 per unit. Therefore, the objective function to maximize profit Z is:
Z=50x+60y
We have the following constraints based on the availability of resistors, transistors, and capacitors:
Each Type A circuit requires 20 resistors and each Type B circuit requires 10 resistors. The total available resistors are 200. Thus, the constraint is:
20x+10y≤200
Simplifying this gives:
2x+y≤20(Constraint 1)
Each Type A circuit requires 10 transistors and each Type B circuit requires 20 transistors. The total available transistors are 120. Thus, the constraint is:
10x+20y≤120
Simplifying this gives:
x+2y≤12(Constraint 2)
Each Type A circuit requires 10 capacitors and each Type B circuit requires 30 capacitors. The total available capacitors are 150. Thus, the constraint is:
10x+30y≤150
Simplifying this gives:
x+3y≤15(Constraint 3)
Since the number of circuits produced cannot be negative, we have:
x≥0,y≥0
Maximize:
Z=50x+60y
Subject to:
2x+y≤20(Constraint 1)x+2y≤12(Constraint 2)x+3y≤15(Constraint 3)x≥0y≥0
To find the corner points of the feasible region, we will solve the equations formed by the constraints:
2x+y=20(1)
x+2y=12(2)
Solving these simultaneously gives (8,4).
x+2y=12(2)
x+3y=15(3)
Solving these simultaneously gives (10.5,1.5).
2x+y=20(1)
x+3y=15(3)
Solving these simultaneously gives (0,20).
- For x=0 in Constraint 1: y=20
- For y=0 in Constraint 1: x=10
- For x=0 in Constraint 2: y=6
- For y=0 in Constraint 2: x=12
- For x=0 in Constraint 3: y=5
- For y=0 in Constraint 3: x=15
Now we will evaluate Z=50x+60y at the corner points:
1. (0,20): Z=50(0)+60(20)=1200
2. (8,4): Z=50(8)+60(4)=400+240=640
3. (10.5,1.5): Z=50(10.5)+60(1.5)=525+90=615
4. (15,0): Z=50(15)+60(0)=750
The maximum profit occurs at the point (15,0) with:
Maximum Profit=750
To maximize profit, the manufacturer should produce:
- 15 circuits of Type A and 0 circuits of Type B.
- The maximum profit will be 750.
Topper's Solved these Questions
- MOCK TEST PAPER -2021 Book:ICSEChapter:MOCK TEST PAPER -2021 Exercise:SECTION -B (15 MARKS )
Explore 10 Videos
- MATRICESBook:ICSEChapter:MATRICESExercise:MULTIPLE CHOICE QUESTION (Competency based questions)
Explore 25 Videos
- MODEL TEST PAPER - 10Book:ICSEChapter:MODEL TEST PAPER - 10Exercise:SECTION - C
Explore 10 Videos
Similar Questions
In the manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistros, 20 transistors and 30 capacitors, If the profit on type A circuit is 50 and that on type B circuit is 60 formulate this problem as LPP, so that hte manufacturer can maximise his profit.
View SolutionWhat are the two types of resistors?
View Solution
Knowledge Check
A 0.2kΩ resistor and 15μF capacitor are connected in series to a 220 V, 50 Hz ac source. The impadance of the circuit is
A250ΩB268ΩC29.15ΩD291.5Ω
In the circuit shown below, the charge on the 60μF capacitor is

View SolutionIn a series AC circuit containing a capacitor and a resistor only
View SolutionA company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionA resistor and an inductor are connected to an ac supply of 120 V and 50 Hz, the current in the circuit is 3 A. If the power consumed in the circuit is 108 W, then the resistance in the circuit is
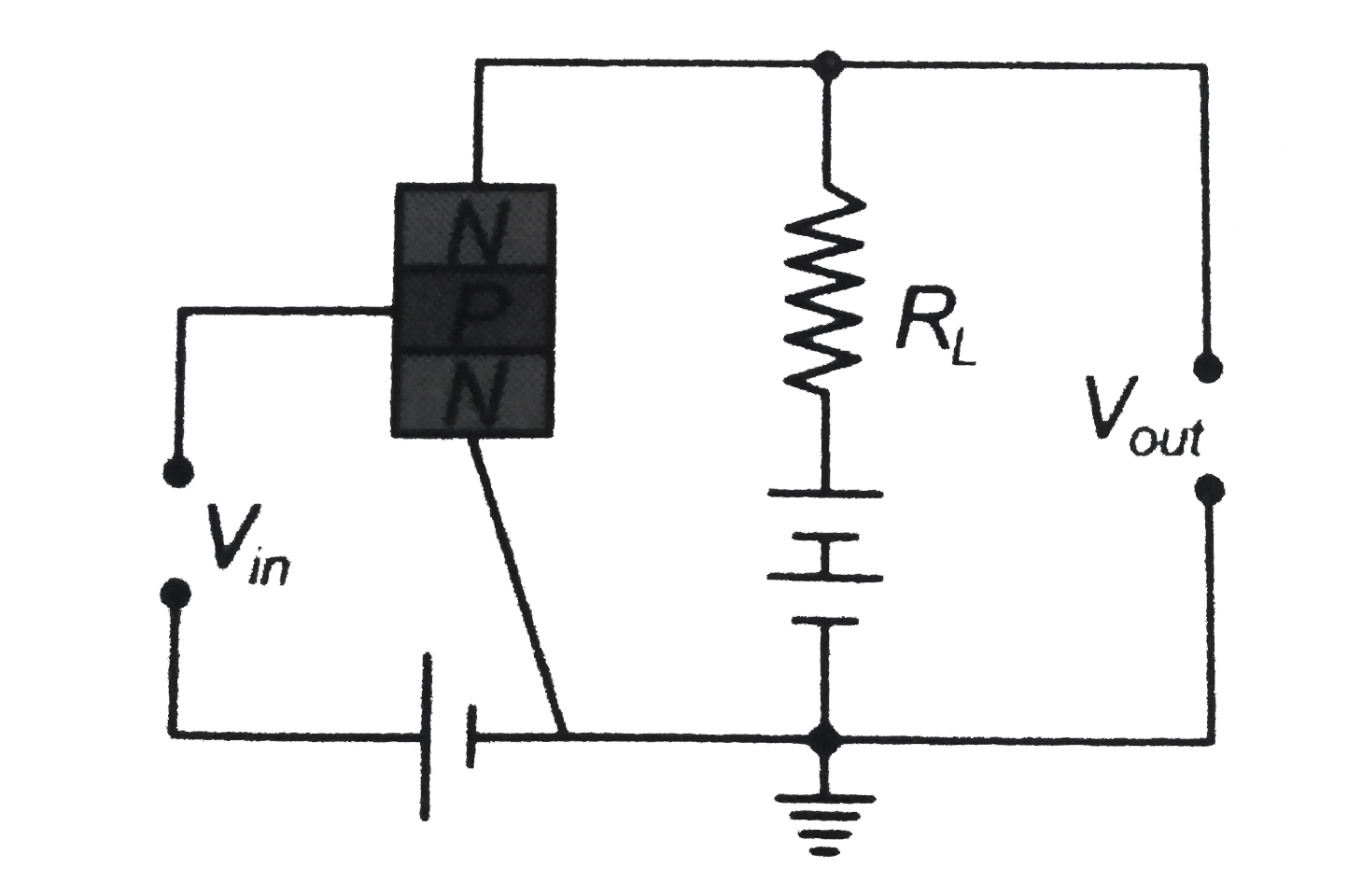
View SolutionAn NPN-transistor circuit is arranged as shown in figure. It is
View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View Solution

