In the manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistros, 20 transistors and 30 capacitors, If the profit on type A circuit is 50 and that on type B circuit is 60 formulate this problem as LPP, so that hte manufacturer can maximise his profit.
The correct Answer is:N/a
To formulate the given problem as a Linear Programming Problem (LPP), we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of units of type A circuits produced
- y = number of units of type B circuits produced
Step 2: Define the Objective Function
The objective is to maximize the profit. The profit from type A circuits is 50x and from type B circuits is 60y. Therefore, the objective function can be written as:
Z=50x+60y
Step 3: Define the Constraints
We need to consider the availability of resistors, transistors, and capacitors.
1. Resistors Constraint:
- Type A requires 20 resistors per unit, and type B requires 10 resistors per unit.
- Total available resistors = 200.
20x+10y≤200
2. Transistors Constraint:
- Type A requires 10 transistors per unit, and type B requires 20 transistors per unit.
- Total available transistors = 120.
10x+20y≤120
3. Capacitors Constraint:
- Type A requires 10 capacitors per unit, and type B requires 30 capacitors per unit.
- Total available capacitors = 150.
10x+30y≤150
Step 4: Non-negativity Constraints
Since the number of circuits produced cannot be negative, we have:
x≥0,y≥0
Final Formulation
The Linear Programming Problem can be summarized as follows:
Maximize:
Z=50x+60y
Subject to:
20x+10y≤200(Resistors)10x+20y≤120(Transistors)10x+30y≤150(Capacitors)x≥0y≥0
Let:
- x = number of units of type A circuits produced
- y = number of units of type B circuits produced
The objective is to maximize the profit. The profit from type A circuits is 50x and from type B circuits is 60y. Therefore, the objective function can be written as:
Z=50x+60y
We need to consider the availability of resistors, transistors, and capacitors.
- Type A requires 20 resistors per unit, and type B requires 10 resistors per unit.
- Total available resistors = 200.
20x+10y≤200
- Type A requires 10 transistors per unit, and type B requires 20 transistors per unit.
- Total available transistors = 120.
10x+20y≤120
- Type A requires 10 capacitors per unit, and type B requires 30 capacitors per unit.
- Total available capacitors = 150.
10x+30y≤150
Since the number of circuits produced cannot be negative, we have:
x≥0,y≥0
The Linear Programming Problem can be summarized as follows:
Z=50x+60y
20x+10y≤200(Resistors)10x+20y≤120(Transistors)10x+30y≤150(Capacitors)x≥0y≥0
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR PROGRAMMINGExercise:OBJECTIVE
Explore 8 Videos
- LINEAR PROGRAMMINGBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR PROGRAMMINGExercise:FILLERS
Explore 7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Fillers
Explore 18 Videos
- MATRICESBook:NCERT EXEMPLAR ENGLISHChapter:MATRICESExercise:Solved example
Explore 101 Videos
Similar Questions
A manufacturer of clectronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is 50 and that on type B circuit is 60, formulate this problem as a LPP do that the manufacturer can maximise his profit. How many of circuits of Type A and of type B, should be produced by the manufacturer so as to maximise his profit? Determine the maximum profit.
View SolutionWhat are the two types of resistors?
View SolutionDetermine to charge on the capacitor in the following circuit :
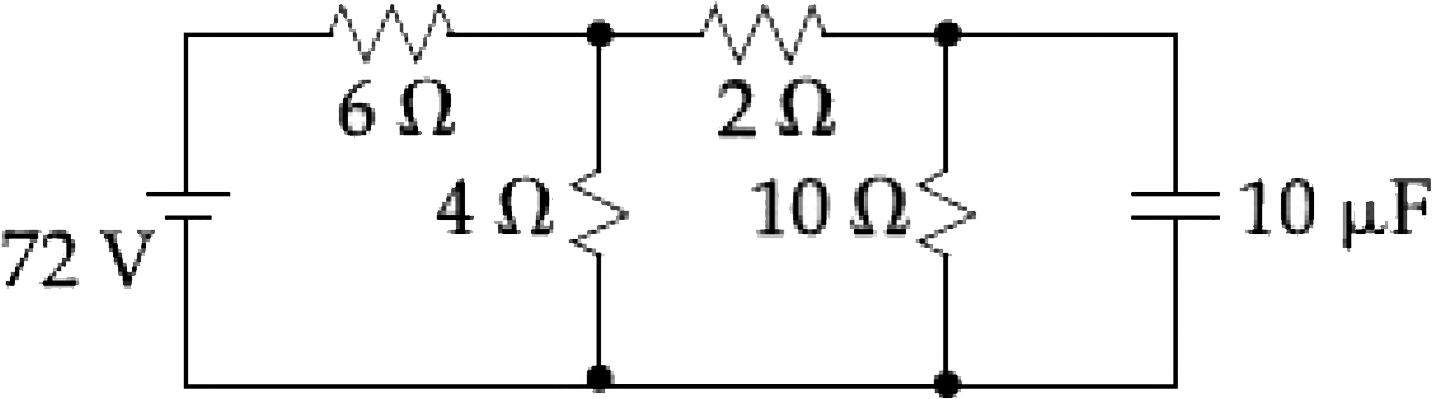
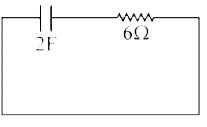
View SolutionIf the capacitor shown in the circuit is charged to 5V and left in the circuit, in 12s the charge on the capacitor will become:
View SolutionWrite the condition required for a circuit to be a closed circuit.
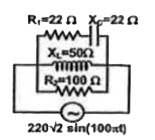
View SolutionThe current through the capacitor in the given circuit is
View SolutionConsider the circuit shwon in fig. The circuit is in steady state.

The charge in capacitor is
View SolutionIn a series AC circuit containing a capacitor and a resistor only
View SolutionIn the following transistor amplifier circuit β=50.Vce→ of the transistor is
View SolutionThe charge on the capacitor of capacitance 10μF in steady state condition in the circuit shown is
_PHY_E05_271_Q01.png)
View Solution

