A resistor and an inductor are connected to an ac supply of 120 V and 50 Hz, the current in the circuit is 3 A. If the power consumed in the circuit is 108 W, then the resistance in the circuit is
(A) 12Ω
(B) 40Ω
(C) √(52×28)Ω
(D) 360Ω
The correct Answer is:A
To find the resistance in the circuit, we can follow these steps:
1. Identify the Given Values:
- Voltage (V) = 120 V
- Frequency (f) = 50 Hz (not directly needed for this calculation)
- Current (I) = 3 A
- Power (P) = 108 W
2. Understand the Power Consumption in the Circuit:
- In an AC circuit with a resistor and an inductor, the power consumed is primarily due to the resistor. The inductor does not consume power; it only stores energy temporarily.
3. Use the Power Formula:
- The power consumed in a resistive circuit can be calculated using the formula:
P=I×VRMS
- However, since we are interested in finding resistance, we can rearrange the formula to express power in terms of resistance:
P=I2×R
4. Rearranging the Formula to Find Resistance:
- From the equation P=I2×R, we can solve for resistance R:
R=PI2
5. Substituting the Known Values:
- Now, substitute the values of power and current into the equation:
R=108W(3A)2
6. Calculating the Resistance:
- Calculate I2:
(3A)2=9A2
- Now substitute this back into the equation for resistance:
R=108W9A2=12Ω
7. Final Answer:
- The resistance in the circuit is R=12Ω.
- Voltage (V) = 120 V
- Frequency (f) = 50 Hz (not directly needed for this calculation)
- Current (I) = 3 A
- Power (P) = 108 W
- In an AC circuit with a resistor and an inductor, the power consumed is primarily due to the resistor. The inductor does not consume power; it only stores energy temporarily.
- The power consumed in a resistive circuit can be calculated using the formula:
P=I×VRMS
- However, since we are interested in finding resistance, we can rearrange the formula to express power in terms of resistance:
P=I2×R
- From the equation P=I2×R, we can solve for resistance R:
R=PI2
- Now, substitute the values of power and current into the equation:
R=108W(3A)2
- Calculate I2:
(3A)2=9A2
- Now substitute this back into the equation for resistance:
R=108W9A2=12Ω
- The resistance in the circuit is R=12Ω.
Topper's Solved these Questions
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Multiple Correct
Explore 5 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Assertion-reasoning
Explore 7 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Exercises Subjective
Explore 15 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
Similar Questions
A resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View Solution
Knowledge Check
A 44 mH inductor is connected to 220 V, 50 Hz ac supply. The rms value of the current in the circuit is
A12.8AB13.6AC15.9AD19.5AA 30μF capacitor is connected to a 150 V, 60 Hz ac supply. The rms value of current in the circuit is
A17 AB1.7AC1.7mAD2.7A
A resistor and capacitor are connected to an ac supply of 200 V, 50 Hz in series. The current in the circuit is 2 A. If the power consumed in the circuit is 100 W then in the above question, the capacitive reactance in the circuit is
View SolutionA 44 mH inductor is connected to 220 V, 50 Hz a.c. supply. Determine rms value of current in the circuit.
View SolutionA coil is series with a 20μF capacitor across a 230V,50Hz supply. The current taken by the circuit is 8A and the power consumed is 200W. Calculate the inductance of the coil if the current in the circuit is
(a) leading
(b) lagging
View SolutionAn 8 H inductor, a 2 μF capacitor and a 100 Ω resistor are connected in series to an A.C. supply of 220 V and 50 Hz. Calculate :
(i) Impedance of the circuit.
(ii) Current flowing through the circuit.
(iii)Phase difference between the current and the supply voltage.
(iv) Average power consumed by the circuit.
View SolutionA 0.21 H inductor and a 12Ω resistance are connected in series to a 220 V, 50 Hz ac source.
The current in the circuit is
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
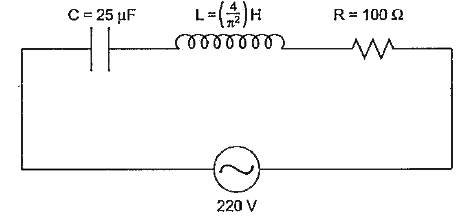
Average power consumed by the circuit.
View Solution