A transmitter transmits at a wavelength of 300 m. A condenser of capacitance 2.4(μ)F is being used. The value of the inductance for the resonant circuit is approximately
(A) 10−4H
(B) 10−6H
(C) 10−8H
(D) 10−10H
The correct Answer is:C
To find the value of the inductance L for the resonant circuit, we can follow these steps:
Step 1: Calculate the frequency of the signal
The frequency f can be calculated using the formula:
f=Cλ
where:
- C is the speed of light, approximately 3×108m/s
- λ is the wavelength, given as 300m
Substituting the values:
f=3×108300=106Hz
Step 2: Use the resonant frequency formula
At resonance, the frequency f is related to the inductance L and capacitance C by the formula:
f=12π√LC
Step 3: Rearranging the formula to find L
Rearranging the formula to solve for L:
L=1(2πf)2C
Step 4: Substitute the values of f and C
We know:
- f=106Hz
- C=2.4μF=2.4×10−6F
Substituting these values into the equation:
L=1(2π×106)2×(2.4×10−6)
Step 5: Calculate L
Calculating (2π×106)2:
(2π×106)2≈(6.2832×106)2≈39.4784×1012
Now substituting this back into the equation for L:
L=139.4784×1012×2.4×10−6=19.474576×106≈1.057×10−8H
Final Result
Thus, the value of the inductance L is approximately:
L≈10−8H
The frequency f can be calculated using the formula:
f=Cλ
where:
- C is the speed of light, approximately 3×108m/s
- λ is the wavelength, given as 300m
f=3×108300=106Hz
At resonance, the frequency f is related to the inductance L and capacitance C by the formula:
f=12π√LC
Rearranging the formula to solve for L:
L=1(2πf)2C
We know:
- f=106Hz
- C=2.4μF=2.4×10−6F
L=1(2π×106)2×(2.4×10−6)
Calculating (2π×106)2:
(2π×106)2≈(6.2832×106)2≈39.4784×1012
L=139.4784×1012×2.4×10−6=19.474576×106≈1.057×10−8H
Thus, the value of the inductance L is approximately:
L≈10−8H
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct
5 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Subjective
15 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
An electro magnetic wave of wavelength 300 metre can be transmitted by a transmission centre. A condenser of capacity 2.5μF is available. Calculate the inductance of the required coil for a resonant circuit.Use π2=10.
View SolutionThe charge on the condenser of capacitance 2μF in the following circuit will be -
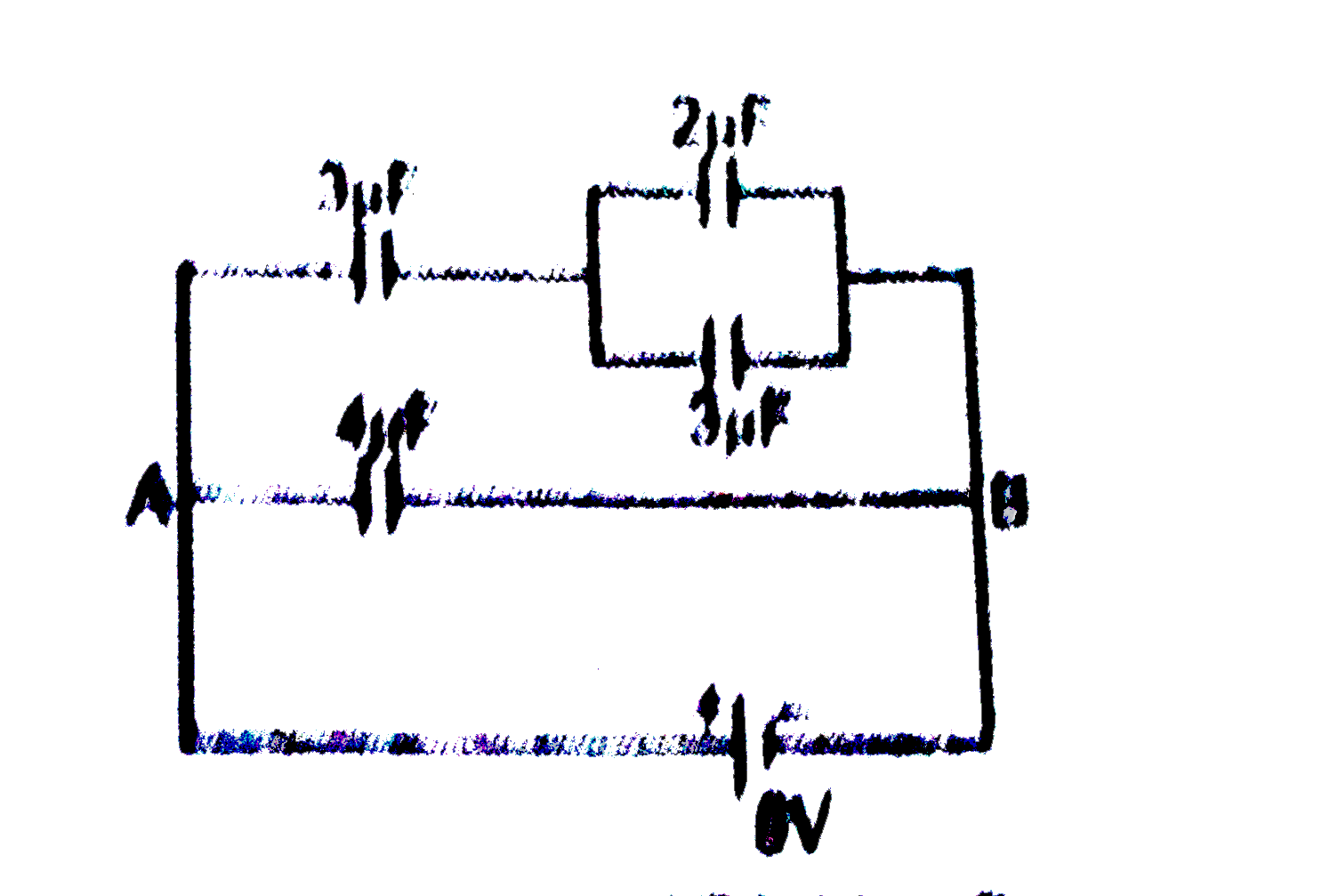
View Solution
Knowledge Check
A circuit consists of a resistance 10 ohm and a capacitance of 0.1μF If an alternating e.m.f. of 100 V. 50 Hz is applied, calculate the current in the circuit.
A3.14mAB6.28mAC1.51mAD7.36mA
A radio transmitter at position A operates at a wavelength of 20m. A second , identical transmitter is located at a distance x from the first transmitter , at position B. The transmitters are phase locked together such that the second transmitter is lagging π/2 out of phase with the first . For which of the following values of BC−CA will the intensity at C be maximum .
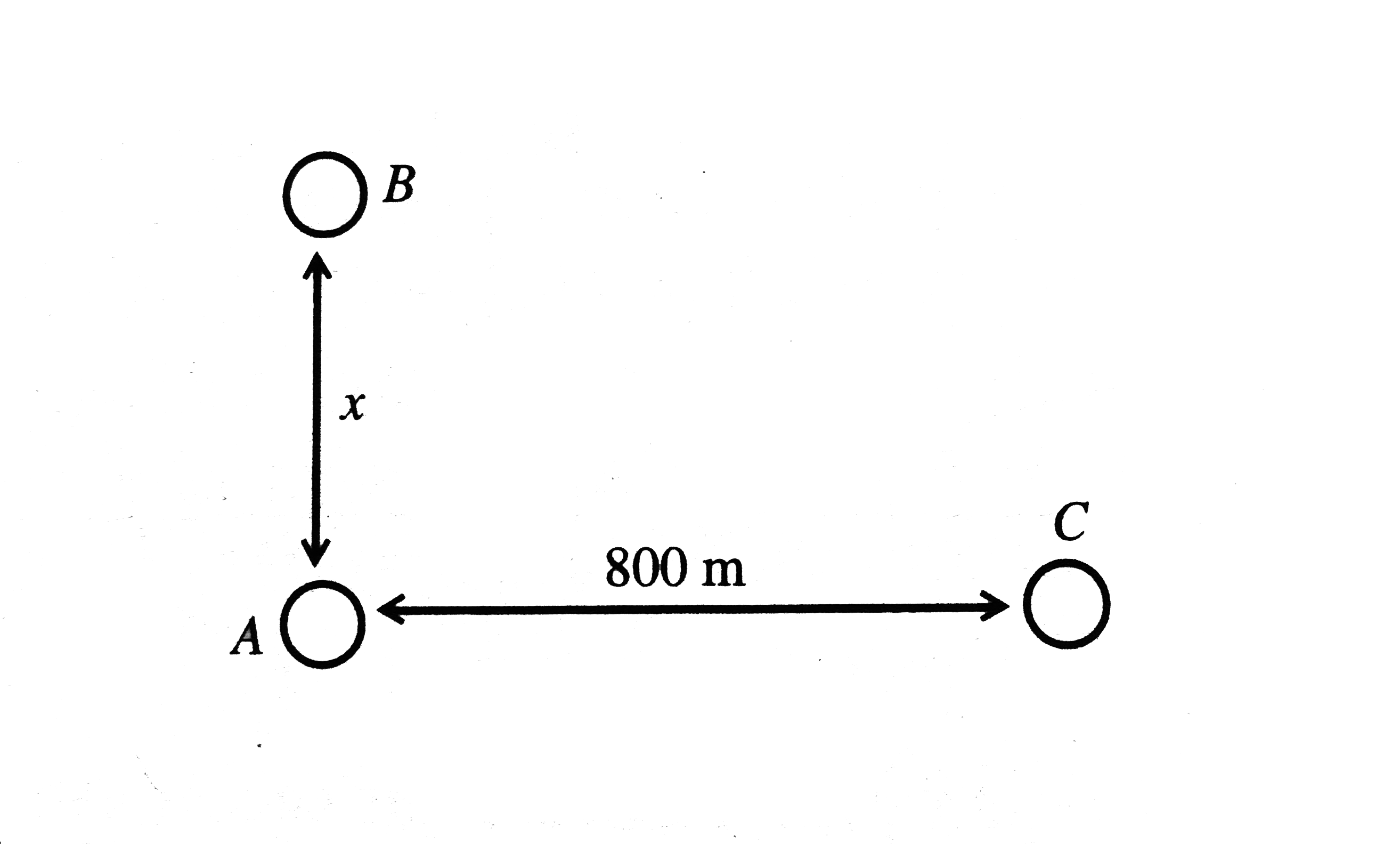
View SolutionIn an ac circuit , an alternating voltage e=200√2sin100t volts is connected to a capacitor of capacitance 1μF. The rms value of the current in the circuit is :
View SolutionIn an AC circuit , an alternating voltage e = 200√2 sin 100t V is connected to a capacitor of capacity 1μF . The rms value of the current in the circuit is
View SolutionAn AC rms voltage of 2V having a frequency of 50 KHz is applied to a condenser of capacity of 10μF. The maximum value of the magnetic field between the plates of the condenser if the radius of plate is 10cm is
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
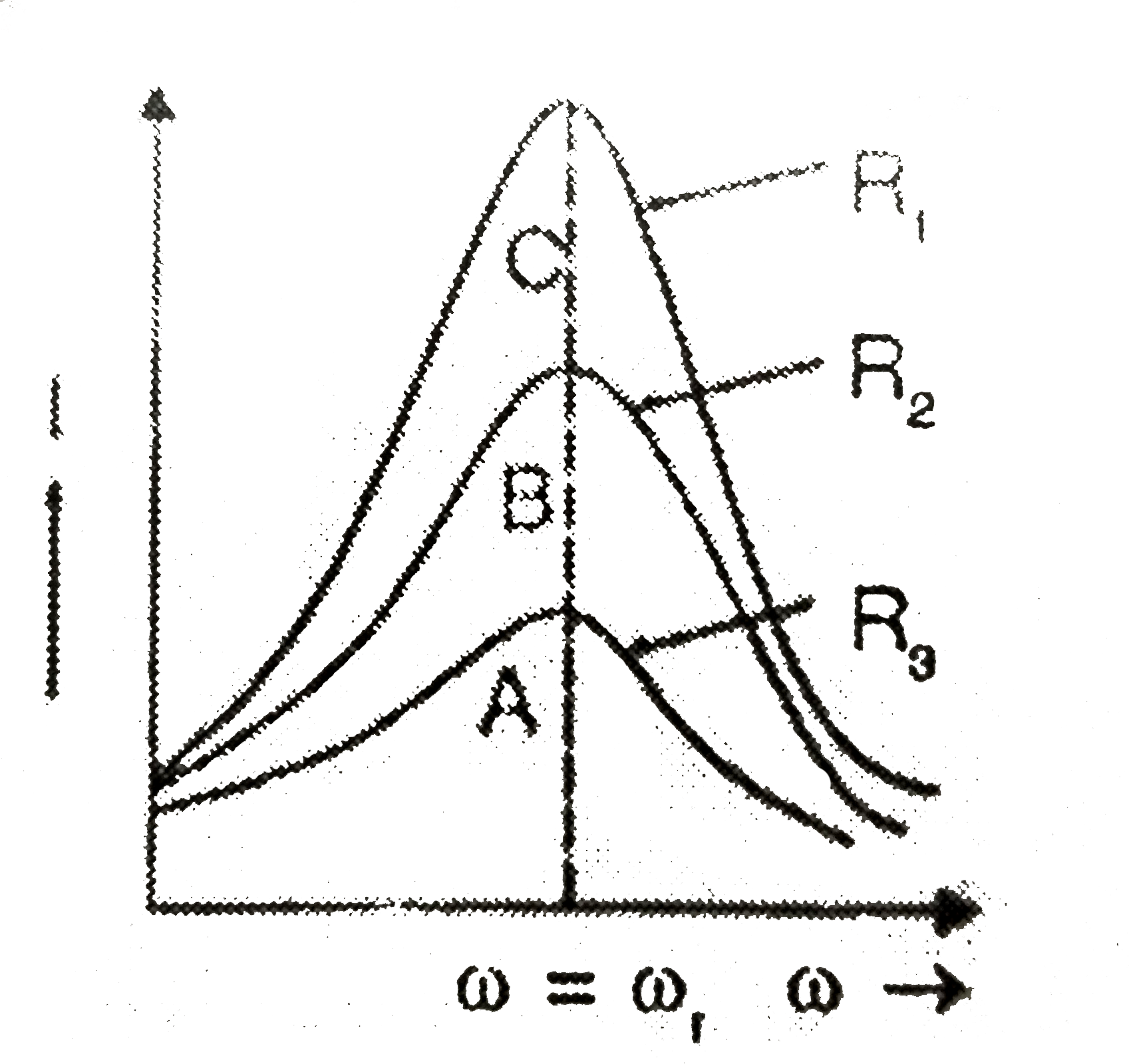
View SolutionA condenser of capacity 1 μ F and a resistance 0.5 mega-ohm are connected in series with a DC supply of 2 V. The time constant of circuit is
View SolutionThe resonant frequency of a circuit is f. If the capacitance is made 4 times the initial values, then the resonant frequecy will become
View Solution
