On a see saw, two chlidren of masses of 30kg and 50kg are sitting on one side of at distances 2m and 2.5m respectively from its middle. Where should a man of mass 74 kg sit to balance it?
To solve the problem of balancing the seesaw with the given masses and distances, we can follow these steps:
1. Identify the Forces and Distances:
- The first child has a mass of 30 kg and is sitting 2 m from the center.
- The second child has a mass of 50 kg and is sitting 2.5 m from the center.
- The man has a mass of 74 kg, and we need to find the distance (let's call it x) from the center where he should sit to balance the seesaw.
2. Calculate the Moments:
- The moment (or torque) is calculated as the product of the mass and the distance from the pivot point (center of the seesaw).
- For the two children, the moments are:
- Moment due to the first child: 30kg×2m=60kg m
- Moment due to the second child: 50kg×2.5m=125kg m
3. Total Moment on One Side:
- The total moment produced by the two children on one side of the seesaw is:
Total Moment=60kg m+125kg m=185kg m
4. Set Up the Equation for Balance:
- To balance the seesaw, the moment produced by the man must equal the total moment produced by the children:
74kg×x=185kg m
5. Solve for x:
- Rearranging the equation gives:
x=185kg m74kg≈2.5m
6. Conclusion:
- The man should sit approximately 2.5 m from the center of the seesaw to balance it.
Final Answer:
The man should sit at a distance of 2.5 meters from the center of the seesaw.
---
- The first child has a mass of 30 kg and is sitting 2 m from the center.
- The second child has a mass of 50 kg and is sitting 2.5 m from the center.
- The man has a mass of 74 kg, and we need to find the distance (let's call it x) from the center where he should sit to balance the seesaw.
- The moment (or torque) is calculated as the product of the mass and the distance from the pivot point (center of the seesaw).
- For the two children, the moments are:
- Moment due to the first child: 30kg×2m=60kg m
- Moment due to the second child: 50kg×2.5m=125kg m
- The total moment produced by the two children on one side of the seesaw is:
Total Moment=60kg m+125kg m=185kg m
- To balance the seesaw, the moment produced by the man must equal the total moment produced by the children:
74kg×x=185kg m
- Rearranging the equation gives:
x=185kg m74kg≈2.5m
- The man should sit approximately 2.5 m from the center of the seesaw to balance it.
The man should sit at a distance of 2.5 meters from the center of the seesaw.
Topper's Solved these Questions
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1A
Explore 27 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Multiple choice questions
Explore 2 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
A boy of mass 30 kg is sitting at a distance of 2 m from the middle of a see-saw. Where should a boy of mass 40 kg sit so as to balance the see-saw ?
View SolutionTwo bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
View Solution
Knowledge Check
Karan of mass 45kg and Geeta of mass 30kg are sitting on a see saw at a distance of 2m and 1.5m respectively from the centre of the see saw in an amusement park as shown in the figure. Is the see saw in rotational equilibrium?
 AYesBNoCdata incompleteDNone of the above
AYesBNoCdata incompleteDNone of the above
Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionThree children are sitting on a see-saw in such a way that is balances. A 20kg and a 30kg boy are on opposite sides at a distance of 2m from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
View SolutionTwo spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
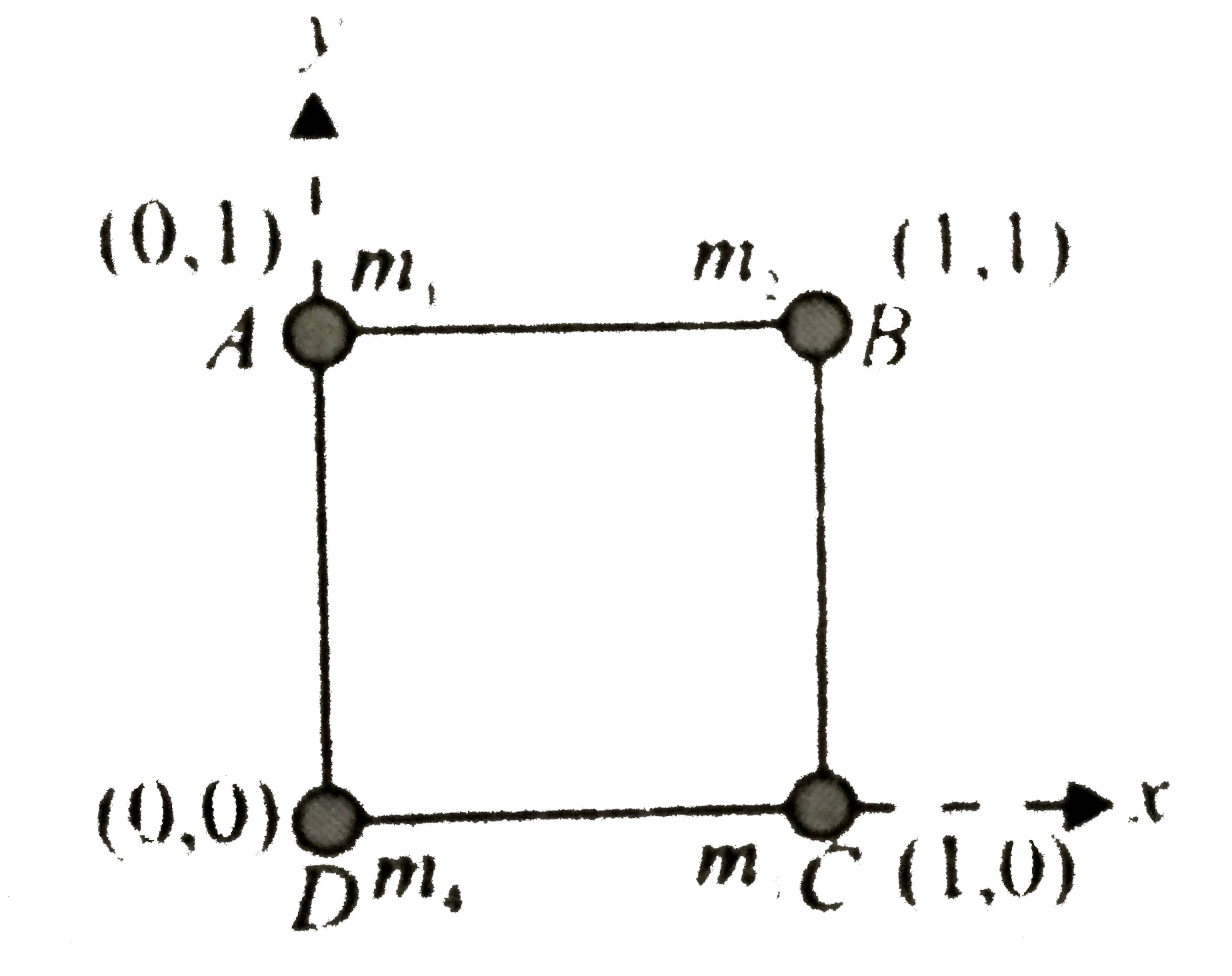
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionThree bodies having masses 5 kg, 4 kg and 2 kg is moving at the speed of 5 m/sand2m//s and 5 m/s respectively along X-axis.The magnitude of velocity of centre of mass is
View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
View SolutionInfinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be
View Solution

