State the condition when on applying a force, a body has:
(a) translational motion, (b) rotational motion
(a) When the body is free to move
(b) When the body is pivoted at a point
Topper's Solved these Questions
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Multiple choice questions
Explore 2 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1(A) Numericals
Explore 18 Videos
- FORCE Book:ICSEChapter:FORCE Exercise:EXERCISE 1( C) Multiple Choice questions
Explore 2 Videos
- ELECTRO-MAGNETISM Book:ICSEChapter:ELECTRO-MAGNETISM Exercise:EXERCISE-10 (C) NUMERICALS
Explore 1 Video
- HOUSEHOLD CIRCUITS Book:ICSEChapter:HOUSEHOLD CIRCUITS Exercise:EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
Knowledge Check
Analogue of mass in rotational motion is.
Amoment of inertiaBtorqueCradius of gyrationDangular momentumA couple produces: a) purely translational motion b) purely rotational motion c) both translational and rotational motion d) no motion
Apurely translational motionBpurely rotational motionCboth translational and rotational motionDno motion
Analogue of mass in rotational motion is
View SolutionState the laws of motion for rotating bodies.
View SolutionA 'T' shaped object with dimensions shown in the figure, is lying on a smooth floor. A force '→F' is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect C.
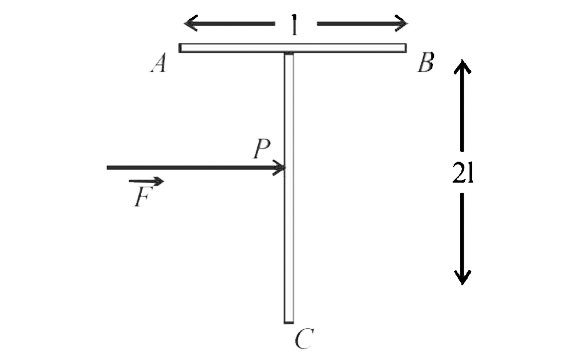
View SolutionA 'T' shaped object with dimensions shown in the figure, is lying on a smooth floor. A force '→F' is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect C.

View SolutionAssertion : The condition of equilibrium for a rigid body is
Translational equilibrium ΣF=0 and
Rotational equilibrium Στ=0
Reason : A rigid body musy be in equilibrium under the action of two equal and opposite forces.
View SolutionA solid sphere is in rolling motion. In rolling motion a body prosseses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simutaneously. The ratio
Kt:(Kt+Kr) for the sphere is
View Solution

