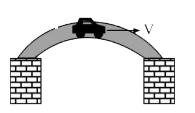
A bridge over a canal is in the form of an arc of a circle of radius 20 m. Calculate the maximum speed at which a motor cycle can pass over the bridge without leaving the ground at the highest point ?.
To solve the problem of finding the maximum speed at which a motorcycle can pass over a bridge in the form of an arc of a circle without leaving the ground at the highest point, we can follow these steps:
1. Understand the Forces at the Highest Point:
At the highest point of the arc, the forces acting on the motorcycle are:
- The gravitational force (weight) acting downwards, which is mg.
- The normal force N acting upwards.
2. Apply the Centripetal Force Condition:
For the motorcycle to stay on the bridge without leaving the ground, the net centripetal force must be equal to the required centripetal force for circular motion. The centripetal force is provided by the difference between the gravitational force and the normal force:
mg−N=mv2r
where:
- m is the mass of the motorcycle,
- v is the speed of the motorcycle,
- r is the radius of the circular arc (20 m).
3. Condition for Leaving the Ground:
The condition for the motorcycle not to leave the ground is that the normal force N must be greater than or equal to zero:
N≥0
This leads to:
mg−mv2r≥0
Rearranging gives:
mg≥mv2r
4. Simplify the Equation:
We can cancel m from both sides (assuming m≠0):
g≥v2r
Rearranging this gives:
v2≤rg
5. Calculate Maximum Speed:
The maximum speed vmax can be expressed as:
vmax=√rg
Substituting the values r=20m and g=9.8m/s2:
vmax=√20×9.8
vmax=√196≈14m/s
Final Answer:
The maximum speed at which a motorcycle can pass over the bridge without leaving the ground at the highest point is approximately 14 m/s.
At the highest point of the arc, the forces acting on the motorcycle are:
- The gravitational force (weight) acting downwards, which is mg.
- The normal force N acting upwards.
For the motorcycle to stay on the bridge without leaving the ground, the net centripetal force must be equal to the required centripetal force for circular motion. The centripetal force is provided by the difference between the gravitational force and the normal force:
mg−N=mv2r
where:
- m is the mass of the motorcycle,
- v is the speed of the motorcycle,
- r is the radius of the circular arc (20 m).
The condition for the motorcycle not to leave the ground is that the normal force N must be greater than or equal to zero:
N≥0
This leads to:
mg−mv2r≥0
Rearranging gives:
mg≥mv2r
We can cancel m from both sides (assuming m≠0):
g≥v2r
Rearranging this gives:
v2≤rg
The maximum speed vmax can be expressed as:
vmax=√rg
Substituting the values r=20m and g=9.8m/s2:
vmax=√20×9.8
vmax=√196≈14m/s
The maximum speed at which a motorcycle can pass over the bridge without leaving the ground at the highest point is approximately 14 m/s.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM BANKING OR RAILS AND ROADS)
Explore 13 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM ANGULAR VELOCITY)
Explore 4 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A national roadway bridge over a canal is in the form of an arc of a circle of radius 49 m. What is the maximum speed with which a car can move without leaving the ground at the highest point? (Take,g=9.8ms−2)
View SolutionA vehicle is moving on an over bridge which is in the form of a circular arc of radius 10 m. What is the maximum speed with which a vehicle can move through the topmost point on the bridge without losing contact with the bridge ? (g=10m/s2)
View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionThe radius of the bump on a road is r. What force does the road exert on a car of mass m when the car passes the highest point on the bump ? Calculate the maximum speed with which the car can pass the highest point before losing contact wtih the road ?
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA motorcycle has to move with a consatnt speed on an overbridge which is in the form of as circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point. a. what can its maximum velocity be for which the contact with the road is not broken at the highest point? b. If the motorcycle goes at speed 1√2 times the maximum found in part a. where will it lose the contact with the road? c. What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
View SolutionA motorcycle has to move with a constant speed on an overbridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.
a. what can its maximum velocity be for which the contact with the road is not broken at the highest point?
b. If the motorcycle goes at speed 1√2 times the maximum found in part a. where will it lose the contact with the road?
c. What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?
View SolutionA car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
View SolutionA car is moving with uniform speed over a circular bridge of radius R which subtends an angle of 90∘ at its center. Find the minimum posible speed so that the car can cross the bridge without losing the contact any where
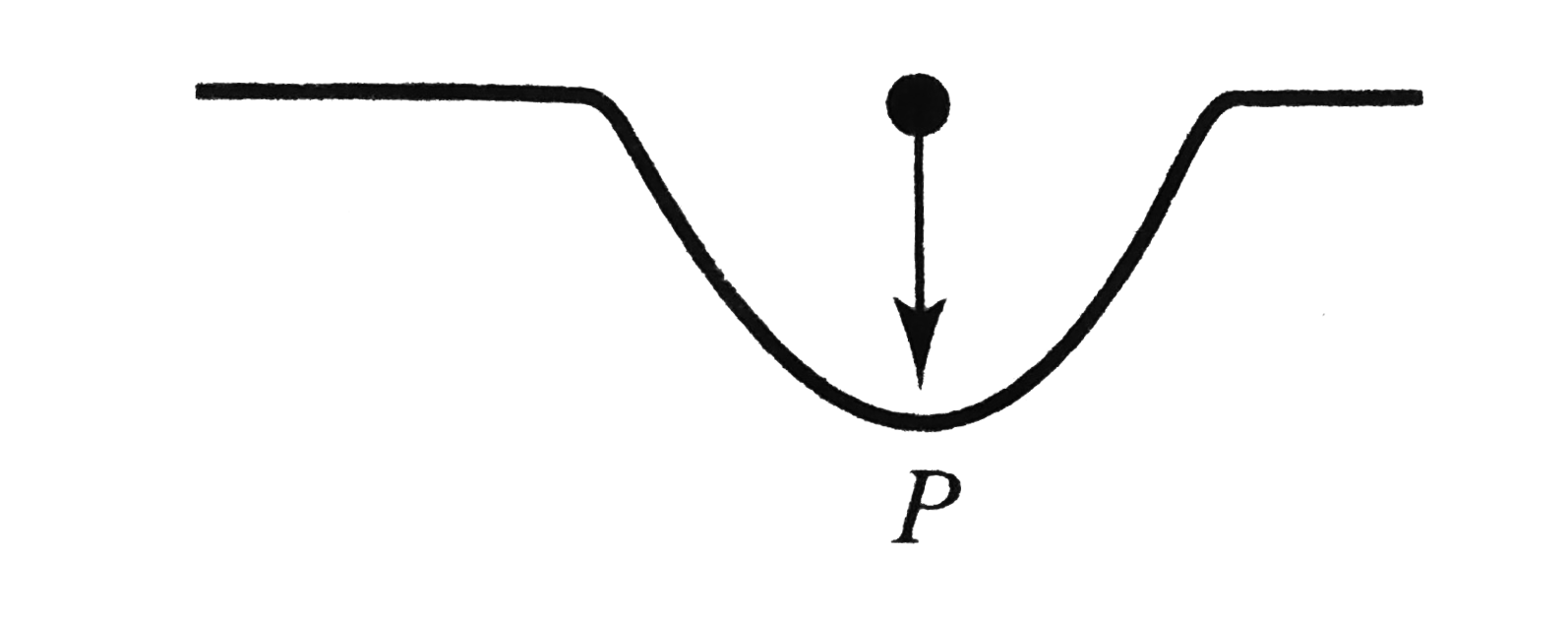
View SolutionA car travelling on a smooth road passes through a curved portion of the road in the form of an arc of circle of radius 10m. If the mass of car is 120kg, find the reaction (in kN) on car at lowest point P where its speed is 20ms−1.
View Solution

