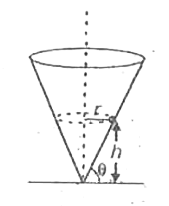
A particle describes a horizontal circle on the smooth surface of an inverted cone, the height of the plane of the circle above the vertex is 9.8 cm. Find the speed of the particle (g= 9.8m/s2) [See Fig.] (a) given in the answer section]
To solve the problem of finding the speed of a particle moving in a horizontal circle on the smooth surface of an inverted cone, we can follow these steps:
Step 1: Understand the Geometry
The height of the circular path above the vertex of the cone is given as h=9.8 cm, which we convert to meters:
h=9.8cm=0.098m
Step 2: Identify Forces Acting on the Particle
The forces acting on the particle are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the cone.
Step 3: Resolve Forces
The normal force can be resolved into two components:
- Nsinθ acts vertically downward and balances the weight of the particle:
Nsinθ=mg
- Ncosθ provides the centripetal force necessary for circular motion:
Ncosθ=mv2r
Step 4: Relate tanθ to g, r, and v
From the above equations, we can express tanθ:
tanθ=NsinθNcosθ=mgmv2r=grv2
Step 5: Find the Relationship Between r and h
Using the geometry of the cone, we can relate the radius r of the circular path to the height h and the angle θ:
tanθ=rh⟹r=htanθ
Step 6: Substitute r in the Equation
Substituting r in the equation for tanθ:
tanθ=g(htanθ)v2
This simplifies to:
v2=ghtanθ
Step 7: Use the Relationship for v
From the earlier expression for v2:
v2=gh
Thus, we can find v:
v=√gh
Step 8: Calculate the Speed
Substituting the values of g and h:
v=√9.8m/s2×0.098m=√0.9604≈0.98m/s
Final Answer
The speed of the particle is approximately:
v≈0.98m/s
---
The height of the circular path above the vertex of the cone is given as h=9.8 cm, which we convert to meters:
h=9.8cm=0.098m
The forces acting on the particle are:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the surface of the cone.
The normal force can be resolved into two components:
- Nsinθ acts vertically downward and balances the weight of the particle:
Nsinθ=mg
- Ncosθ provides the centripetal force necessary for circular motion:
Ncosθ=mv2r
From the above equations, we can express tanθ:
tanθ=NsinθNcosθ=mgmv2r=grv2
Using the geometry of the cone, we can relate the radius r of the circular path to the height h and the angle θ:
tanθ=rh⟹r=htanθ
Substituting r in the equation for tanθ:
tanθ=g(htanθ)v2
This simplifies to:
v2=ghtanθ
From the earlier expression for v2:
v2=gh
Thus, we can find v:
v=√gh
Substituting the values of g and h:
v=√9.8m/s2×0.098m=√0.9604≈0.98m/s
The speed of the particle is approximately:
v≈0.98m/s
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM BANKING OR RAILS AND ROADS)
Explore 13 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM ANGULAR VELOCITY)
Explore 4 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
View SolutionA particle describes a horizontal circle in a conical funne whoses inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
View SolutionA particle describes a horizontal circle in a conical funne whoses inner surface is smooth with speed of 0.5m/s . What is the height of the plane of circle from vertex the funnel?
View SolutionA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The heigh of the plane of motion above the vertex is hh and the semi-vertical angle of the cone is α The period of revolution of the particle

View SolutionThe area of the curved surface of a cone is 60π cm2. If the slant height of the cone be 8cm, find the radius of the base.
View SolutionA particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
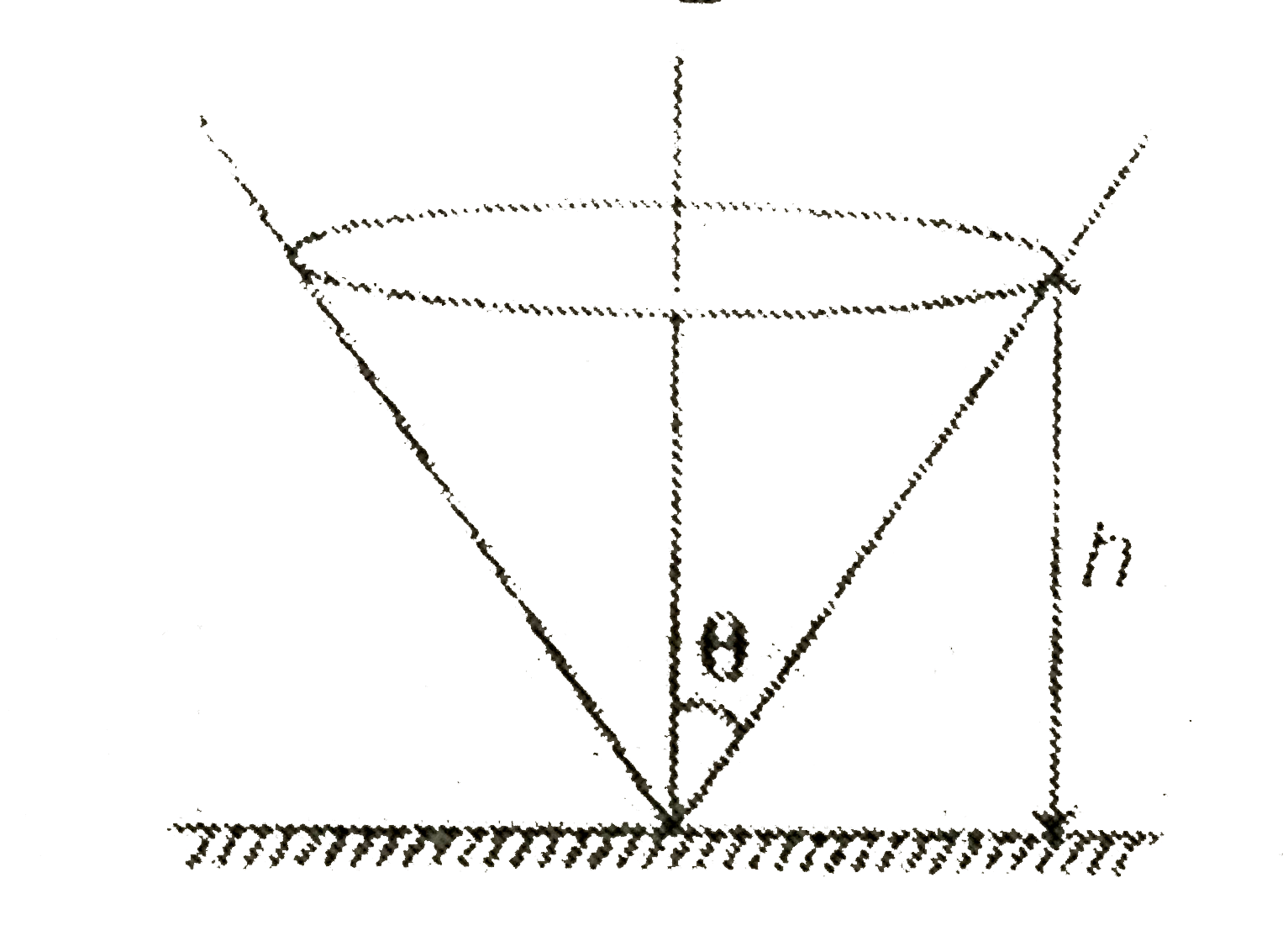
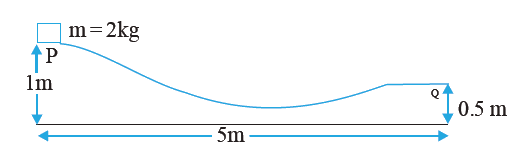
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
View SolutionWhat is the value of g at a height 8848 m above sea level. Given g on the surface of the earth is 9.8ms−2. Mean radius of the earth =6.37×106m.
View SolutionA particle is launched from a height 8R above the surface of earth and it is given a speed (GM8R) parallel to the surfaces then
View SolutionFind the value of 'g(i)' at a height of 100 km (ii) at height 6400 km from the surface of the earth. (Radius of the earth = 6400 km, g on the surface of the earth =9.8ms−2.
View Solution

