A car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
The correct Answer is:A, B, C, D
(a) mg−N1=mv2R ltbr4gt 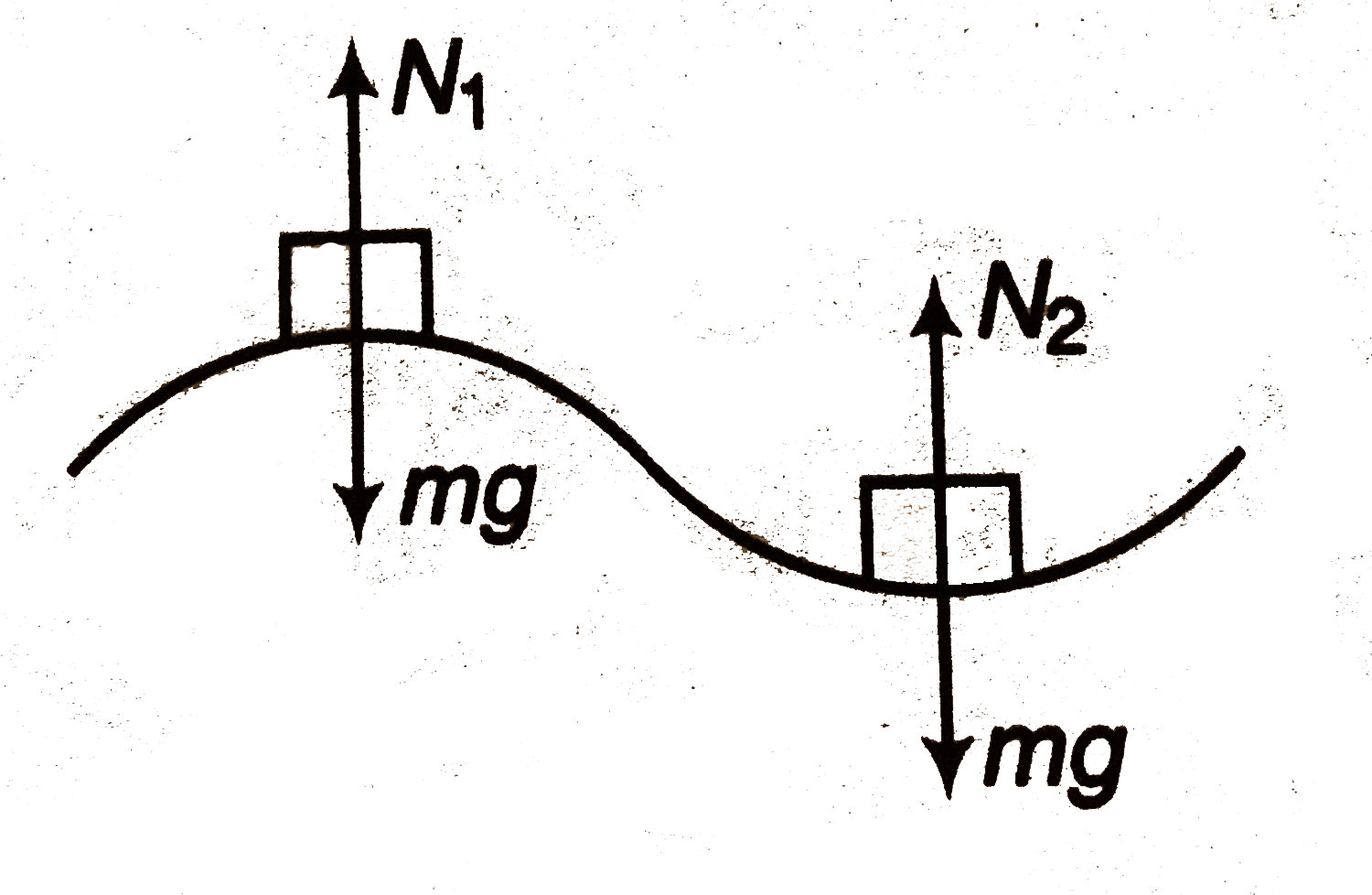
or mg−mg2=mv2R
:. mv2R=mg2=16KN2=8KN
Now, N2−mg=mv2R or N2=mg+mv2R
=mg+mg2+32mg
=32(16KN)=24KN
(b) mg−N=mv2R or N=mg−mv2R
0=mg−mv2maxR
:. vmax=√gR=√10×250=50m/s
(c) N2−mg=mv2R
:. N2=m(g+v2R)
=16×10310[10+2500250]
=32×103N=32KN
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.34videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason28videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.17videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car is NAandNB when it is at the points A and B respectively
 .View Solution
.View SolutionThe radius of the bump on a road is r. What force does the road exert on a car of mass m when the car passes the highest point on the bump ? Calculate the maximum speed with which the car can pass the highest point before losing contact wtih the road ?
View Solution
Knowledge Check
- Question 1 - Select One
A car moving on a straight road is an example of:
Arotatory motionBrectilinear motionCoscillatory motionDperiodic motion - Question 2 - Select One
A car traveled at 80 mph for the first half of the time of a trip and at 40 mph for the second half of the trip. What is the average speed of the car during the entire trip?
A20B40C50D60
A car travels with constant speed on a circular road on level ground. In the figure shown, Fair is the force of air resistance on the car. Which of the other forces best represent the horizontal force of the road on the car's tires ?
 View Solution
View SolutionA car is moving with constant speed on a rough banked road.

Figure shows the free body diagram of car in three situation A, B & C respectively:
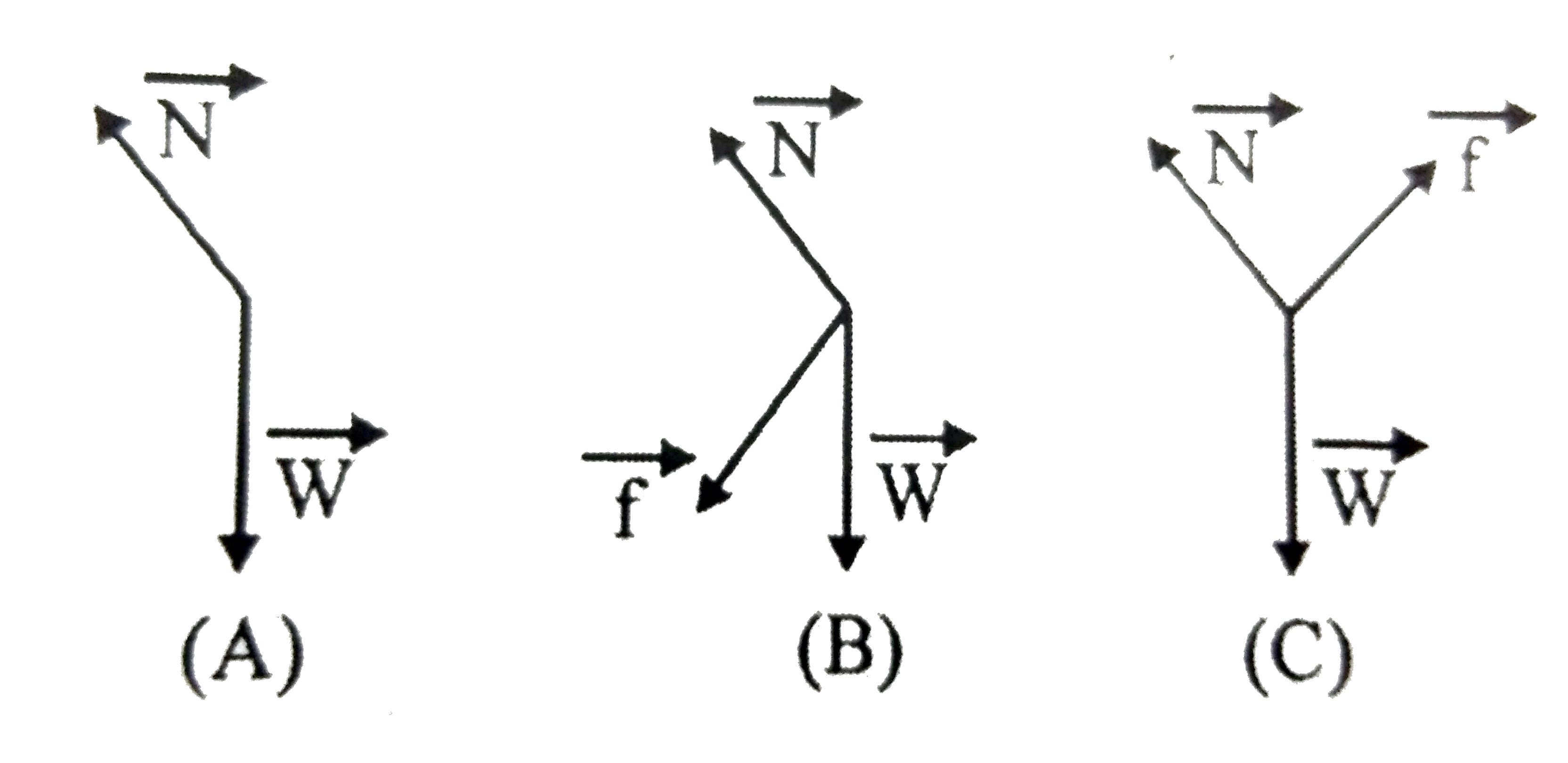 View Solution
View SolutionWhat provides the centripetal force to a car taking a turn on a level road ?
View SolutionA car moving with speed v on a straight road can be stopped with in distance d on applying brakes. If same car is moving with speed 3v and brakes provide half retardation, then car will stop after travelling distance
View SolutionA car travels with constant speed on a circular road level ground in figure Fair is the force of air resistence acts opposite to the motion of car which of the other forces shown best represents the horizontal force of the road on the car's tires?
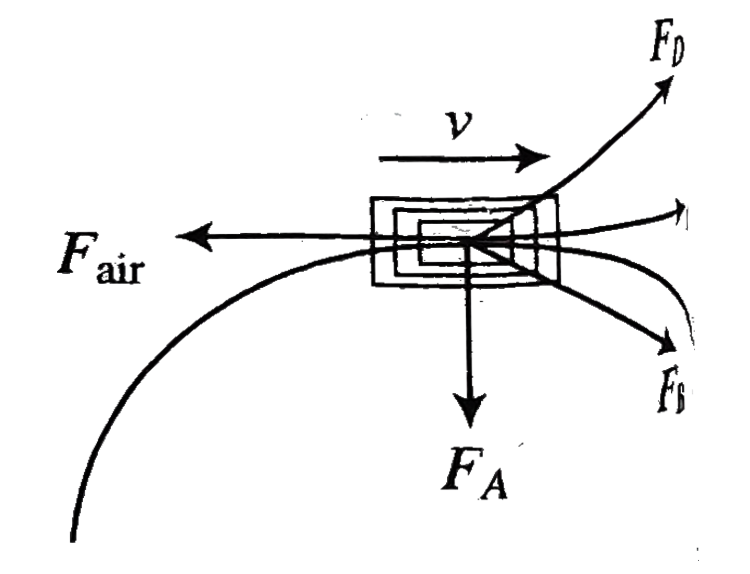 View Solution
View SolutionA car is moving on a straight road covers one third of the distance with a speed of 20 km/h and the rest with a speed of 60 km/h. The average speed of the car is
View Solution
