Question

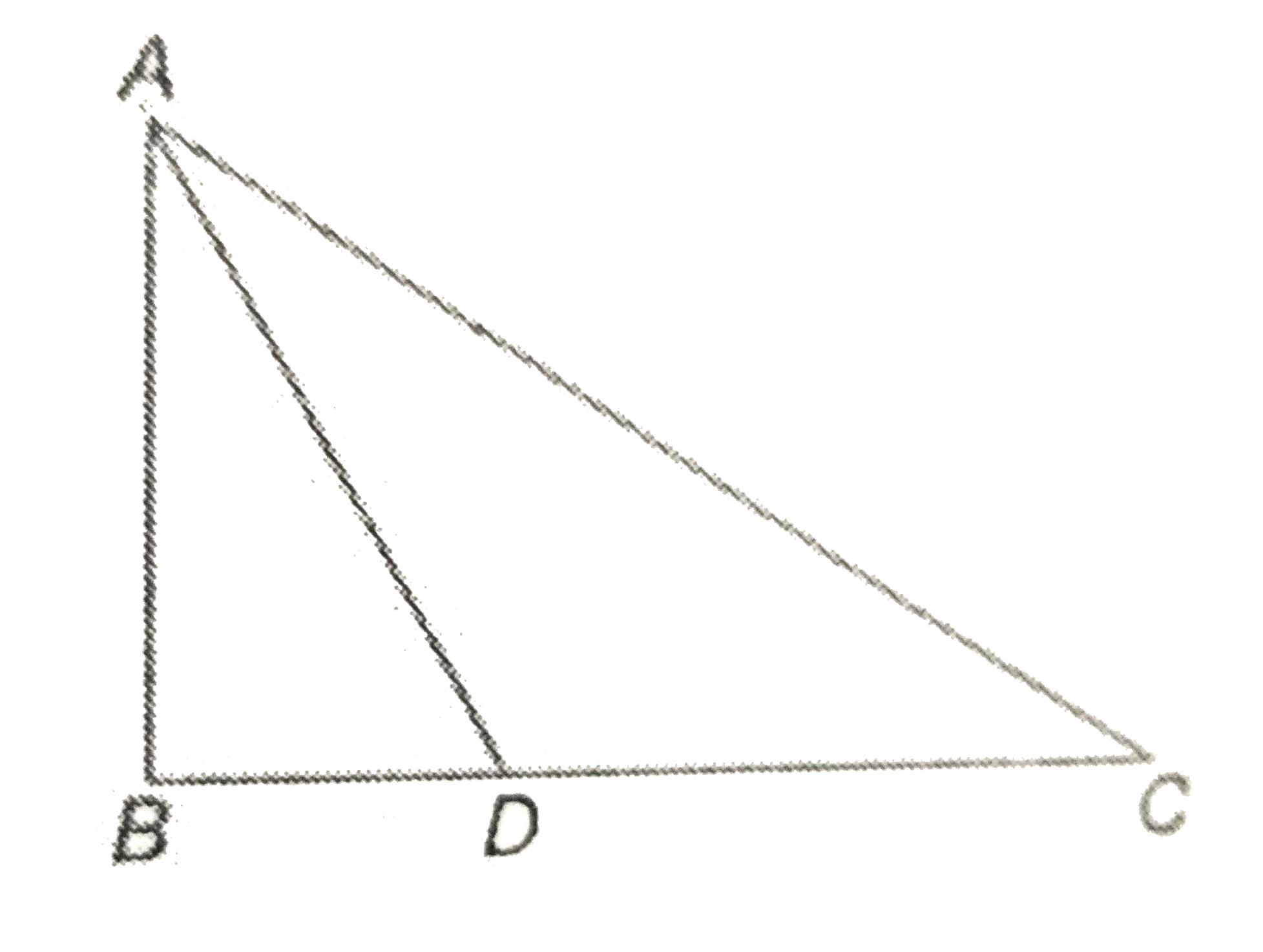
In a triangle ABC, $\angle B={90}^{\circ },AB=8cm,BC=6cm$. BD is perpendicular to AC, then find the length of CD, AD and BD.

Answer

`CD=3.6, AD=6.4, BD=4.8`

Explanation

To solve the problem step by step, we will follow the approach outlined in the video transcript:

Step 1: Identify the triangle and given values
We have a right triangle ABC where:
- Angle B = 90°
- AB = 8 cm
- BC = 6 cm

Step 2: Find the length of AC using the Pythagorean theorem
According to the Pythagorean theorem:
\( AC^2 = AB^2 + BC^2 \)

Substituting the known values:
\( AC^2 = 8^2 + 6^2 \)
\( AC^2 = 64 + 36 \)
\( AC^2 = 100 \)

Now, taking the square root:
\( AC = \sqrt{100} = 10 \text{ cm} \)

Step 3: Find the length of CD using the similarity of triangles
Using the property of similar triangles, we can find CD:
\( CD = \frac{BC^2}{AC} \)

Substituting the known values:
\( CD = \frac{6^2}{10} \)
\( CD = \frac{36}{10} = 3.6 \text{ cm} \)

Step 4: Find the length of AD using the similarity of triangles
Similarly, we can find AD:
\( AD = \frac{AB^2}{AC} \)

Substituting the known values:
\( AD = \frac{8^2}{10} \)
\( AD = \frac{64}{10} = 6.4 \text{ cm} \)

Step 5: Find the length of BD using the formula for the area of the triangle
The length of BD can be found using the formula:
\( BD = \frac{AB \times BC}{AC} \)

Substituting the known values:
\( BD = \frac{8 \times 6}{10} \)
\( BD = \frac{48}{10} = 4.8 \text{ cm} \)

Summary of Results
- CD = 3.6 cm
- AD = 6.4 cm
- BD = 4.8 cm