In a triangle is the midpoint of . Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
The correct Answer is:108
To solve the problem step by step, we will follow the information given and apply the necessary mathematical principles.
Step 1: Identify the given information
We have a right triangle ABC where:
- ∠B=90∘
- D is the midpoint of AC
- BD=√117
- The sum of sides AB+BC=30 cm
Step 2: Find the length of AC
Since D is the midpoint of AC, we can express AC in terms of BD:
AC=2×BD=2×√117
Calculating this gives:
AC=2√117 cm
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
AB2+BC2=AC2
Substituting AC:
AB2+BC2=(2√117)2=4×117=468
This gives us our first equation:
AB2+BC2=468(1)
Step 4: Use the sum of sides equation
We know from the problem statement that:
AB+BC=30(2)
Step 5: Square equation (2)
Squaring both sides of equation (2):
(AB+BC)2=302
Expanding this:
AB2+2AB⋅BC+BC2=900
Substituting AB2+BC2 from equation (1):
468+2AB⋅BC=900
Step 6: Solve for AB⋅BC
Rearranging gives:
2AB⋅BC=900−468=432
Thus:
AB⋅BC=4322=216(3)
Step 7: Find the area of triangle ABC
The area A of triangle ABC can be calculated using:
A=12×AB×BC
Substituting AB⋅BC from equation (3):
A=12×216=108 cm2
Final Answer
The area of triangle ABC is 108 cm2.
---
We have a right triangle ABC where:
- ∠B=90∘
- D is the midpoint of AC
- BD=√117
- The sum of sides AB+BC=30 cm
Since D is the midpoint of AC, we can express AC in terms of BD:
AC=2×BD=2×√117
Calculating this gives:
AC=2√117 cm
According to the Pythagorean theorem:
AB2+BC2=AC2
Substituting AC:
AB2+BC2=(2√117)2=4×117=468
This gives us our first equation:
AB2+BC2=468(1)
We know from the problem statement that:
AB+BC=30(2)
Squaring both sides of equation (2):
(AB+BC)2=302
Expanding this:
AB2+2AB⋅BC+BC2=900
Substituting AB2+BC2 from equation (1):
468+2AB⋅BC=900
Rearranging gives:
2AB⋅BC=900−468=432
Thus:
AB⋅BC=4322=216(3)
The area A of triangle ABC can be calculated using:
A=12×AB×BC
Substituting AB⋅BC from equation (3):
A=12×216=108 cm2
The area of triangle ABC is 108 cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let ABC be a triangle with ∠B=90∘. Let AD be the bisector of ∠A with D on BC. Supose AC = 6 cm and the area of the triangle ADC is 10 cm2 . Then the length of BD in cm is equal to
A35B310C53D103ABC is a triangle in which ∠A=90∘ , AN⊥BC, BC=12 cm and AC=5 cm. Find the ratio of the areas of △ANC and △ABC.
A125:44B25:144C144:25D12:5In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
A16B24C32D36
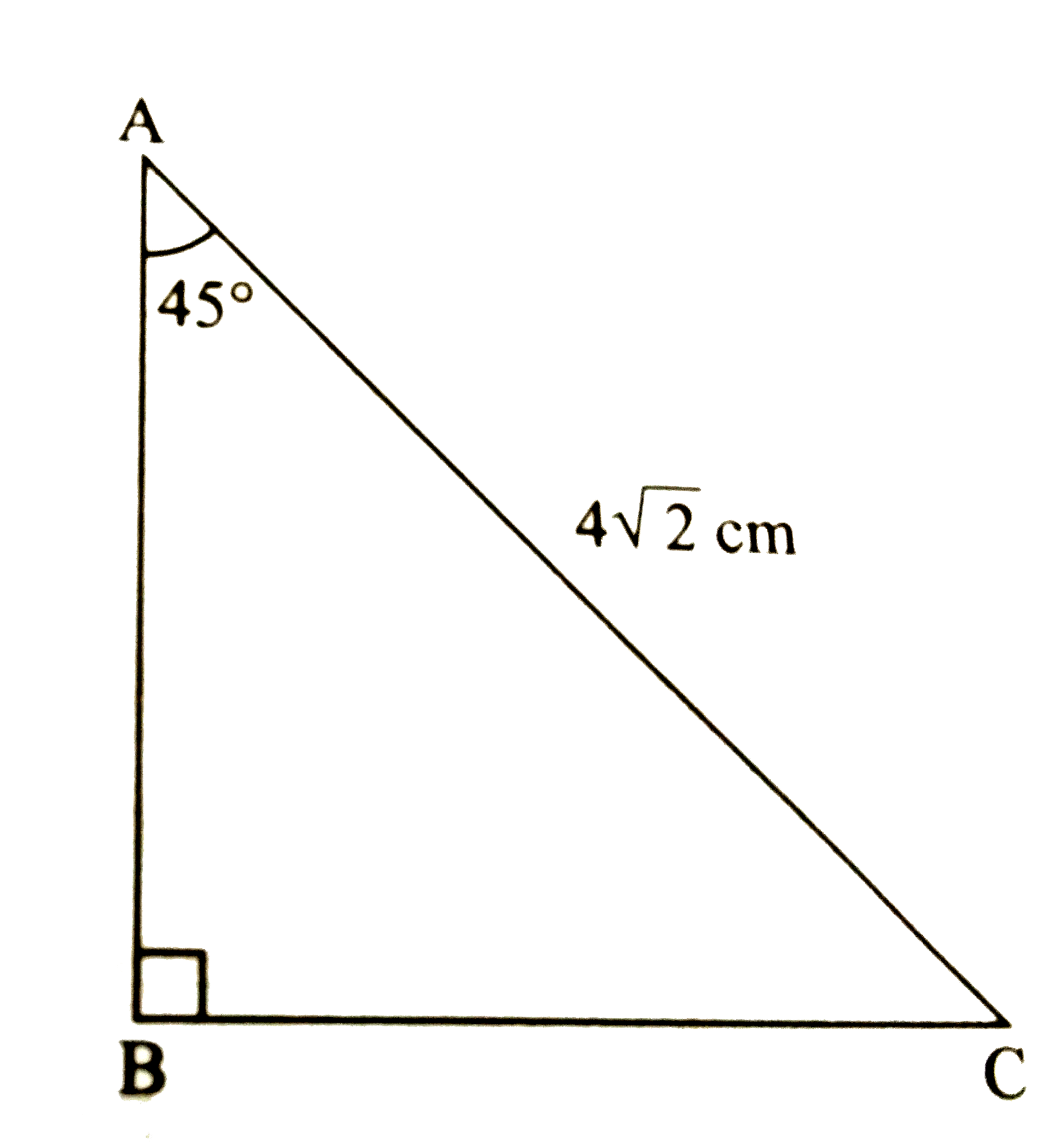
In △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionLet ABC be a triangle with ∠B=900 . Let AD be the bisector of ∠A with D on BC. Suppose AC=6cm and the area of the triangle ADC is 10cm2. Find the length of BD.
View SolutionIn a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?
View SolutionIn an isosceles triangle ABC,∠B=90∘ and side AB=6cm. Side AC will be
View Solution