Question

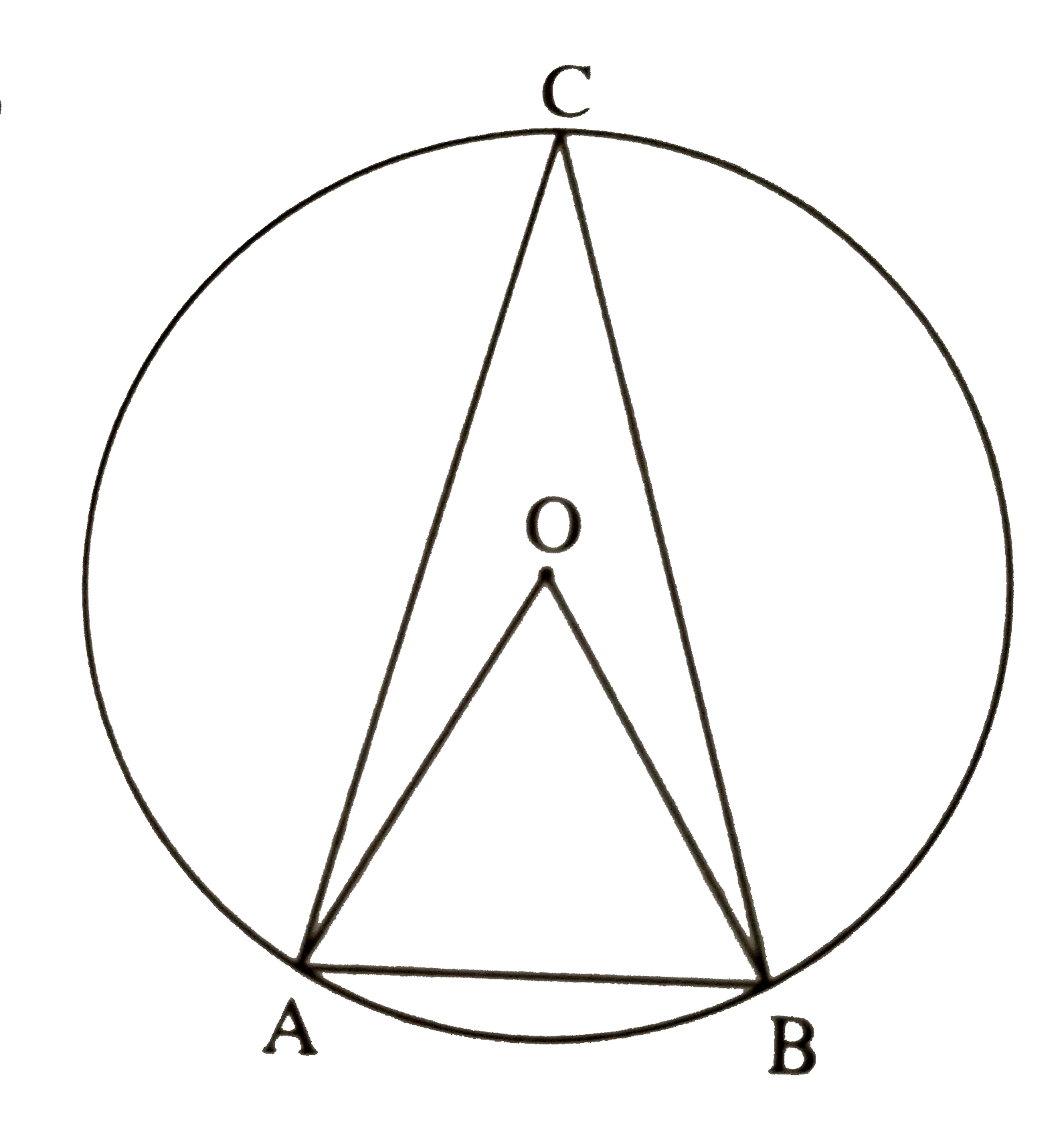
In a circle with centre O, there are two chords AB and Bc, such that $\angle OAB={24}^{\circ }$ and $\angle OCB={42}^{\circ }$. Find the measure of $\angle AOC$

Options

A. `132^@`
B. `63^@`
C. `228^@`
D. EITHER (A) OR ( C )

Answer

D

Explanation

To find the measure of angle AOC in the given circle with center O, we can follow these steps:

1. Identify the Given Angles: We are given:
- \( \angle OAB = 24^\circ \)
- \( \angle OCB = 42^\circ \)

2. Draw the Diagram: Draw a circle with center O. Mark points A, B, and C on the circumference such that AB and BC are two chords.

3. Identify Isosceles Triangles:
- Triangle OAB is isosceles because OA = OB (both are radii of the circle).
- Triangle OCB is also isosceles because OC = OB (both are radii of the circle).

4. Calculate Angles in Triangles:
- In triangle OAB, since OA = OB, we have:
\( \angle OBA = \angle OAB = 24^\circ \)
- Therefore, the remaining angle \( \angle AOB \) can be calculated as:
\( \angle AOB = 180^\circ - \angle OAB - \angle OBA = 180^\circ - 24^\circ - 24^\circ = 132^\circ \)

5. Calculate Angles in Triangle OCB:
- Similarly, in triangle OCB, since OC = OB, we have:
\( \angle OBC = \angle OCB = 42^\circ \)
- Therefore, the remaining angle \( \angle BOC \) can be calculated as:
\( \angle BOC = 180^\circ - \angle OCB - \angle OBC = 180^\circ - 42^\circ - 42^\circ = 96^\circ \)

6. Find Angle AOC:
- Now, we can find angle AOC using the property of angles at the center and the circumference:
\( \angle AOC = \angle AOB + \angle BOC = 132^\circ + 96^\circ = 228^\circ \)

Final Answer:
Thus, the measure of \( \angle AOC \) is \( 228^\circ \).