The radius of a circle is 2 cm, what is its curvature?
A)1 cm
B)4 cm
C)0.5 cm
D)1.414 cm
The correct Answer is:C
To find the curvature of a circle given its radius, we can follow these steps:
Step 1: Understand the formula for curvature
The curvature K of a circle is defined as the reciprocal of its radius r. The formula is:
K=1r
Step 2: Substitute the given radius into the formula
We are given that the radius r of the circle is 2 cm. We will substitute this value into the curvature formula:
K=12 cm
Step 3: Calculate the curvature
Now, we perform the calculation:
K=0.5 cm−1
Step 4: Identify the correct option
From the options provided:
- Option A: 1 cm
- Option B: 4 cm
- Option C: 0.5 cm
- Option D: 1.414 cm
The correct answer is:
Option C: 0.5 cm
Final Answer
The curvature of the circle is 0.5 cm−1.
---
The curvature K of a circle is defined as the reciprocal of its radius r. The formula is:
K=1r
We are given that the radius r of the circle is 2 cm. We will substitute this value into the curvature formula:
K=12 cm
Now, we perform the calculation:
K=0.5 cm−1
From the options provided:
- Option A: 1 cm
- Option B: 4 cm
- Option C: 0.5 cm
- Option D: 1.414 cm
Option C: 0.5 cm
The curvature of the circle is 0.5 cm−1.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The difference between circumference and the radius of a circle is 111 cm. What is the area (in cm2) of the circle?
A469B1386C912D1086If the radius of a circle is 2 cm and is increasing at the rate of 0.5 cm/sec., then the rate of increase of its area is
Aπcm2/secB2πcm2/secC3πcm2/secD4πcm2/secIn the given figure, ABC is a right angled triangle. ∠ABC=90∘and∠ACB=60∘. If the radius of the smaller circle is 2 cm, then what is the radius (in cm) of the larger circle?
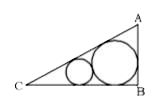 A4B6C4.5D7.5
A4B6C4.5D7.5
The diameter of a circle is 14 cm, find its radius.
View SolutionThe difference in the areas of two concentric circles is 66 cm2 and the radius of the outer circle is 11 cm. What is the radius of the inner circle?
View SolutionIf the circumference of a circle is 22 cm., then what must be its area (in cm2) ?
View SolutionIf the difference between the circumference and diameter of a circle is 30 cm, then what is the radius of the circle ?
View SolutionIf the rate of increase of the radius of a circle is 5 cm/sec, then the rate of increase of its area, when the radius is 20 cm, will be
View Solution
