In a circle with centre O, chords AB and CD intersect inside the circumference at E. Find ∠AEC. If ∠AOC=40∘and∠BOD=50∘.
90∘
45∘
30∘
60∘
The correct Answer is:B
To find the angle AEC in the given circle with center O, we will follow these steps:
Step 1: Identify the angles at the center
We are given:
- Angle AOC = 40°
- Angle BOD = 50°
Step 2: Use the property of angles at the center and circumference
The angle at the center (AOC) is twice the angle at the circumference (ABC) for the same arc. Therefore:
Angle ABC=Angle AOC2=40°2=20°
Step 3: Apply the same property for angle BOD
Similarly, for angle BOD:
Angle BCD=Angle BOD2=50°2=25°
Step 4: Use the exterior angle property in triangle BCE
In triangle BCE, we can use the exterior angle property which states that the exterior angle (AEC) is equal to the sum of the two opposite interior angles (EBC and BCE):
Angle AEC=Angle EBC+Angle BCE
Substituting the values we found:
Angle AEC=20°+25°=45°
Final Answer
Thus, the value of angle AEC is:
Angle AEC=45°
---
We are given:
- Angle AOC = 40°
- Angle BOD = 50°
The angle at the center (AOC) is twice the angle at the circumference (ABC) for the same arc. Therefore:
Angle ABC=Angle AOC2=40°2=20°
Similarly, for angle BOD:
Angle BCD=Angle BOD2=50°2=25°
In triangle BCE, we can use the exterior angle property which states that the exterior angle (AEC) is equal to the sum of the two opposite interior angles (EBC and BCE):
Angle AEC=Angle EBC+Angle BCE
Substituting the values we found:
Angle AEC=20°+25°=45°
Thus, the value of angle AEC is:
Angle AEC=45°
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given diagram, AB is the diameter of the given circle with centre O. C and D are points on the circumference of the circle. If ∠ABD=35∘and∠CDB=15∘, then ∠ CBD equals.
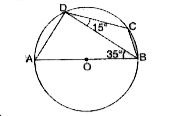 A55∘B75∘C40∘D25∘
A55∘B75∘C40∘D25∘If 76 is divided into four parts proportional to 7, 5, 3, 4, then the smallest part is:
AA) 12BB) 15CB) 15DD) 19In a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
A30∘B25∘C50∘D60∘
In a circle with centre O, chords AB and CD intersect inside the circumference at E. Prove that ∠AOC+ ∠BOD=2 ∠AEC
View SolutionIn a circle with centre O,chords AB and CD intersect inside the circumference at E.Prove that ∠AOC+∠BOD=2∠AEC
View SolutionTwo chords AB and CD intersect at E . The centre of circle is O .∠BOD=50∘and∠AOC=40∘ find ∠AEC
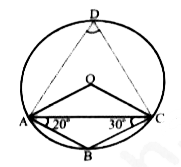
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
View SolutionIn a circle , O is the centre of the circle. Chords AB and CD intersect at P. If ∠AOD=32∘ and ∠COB=26∘, then the measure of ∠APD lies between:
केंद्र O के साथ एक वृत्त में, जीवा AB और CD,P पर प्रतिच्छेद करते हैं, यदि ∠AOD=32∘ और ∠COB=26∘ तो ∠APD का माप किसके बीच में होगा
View Solution