Through any given set of four points P,Q,R,S it is possible to draw
1. atmost one circle
2. exactly one circle
3. exactly two circles
4. exactly three circles
The correct Answer is:A
To solve the problem of how many circles can be drawn through any given set of four points P, Q, R, and S, we can follow these steps:
Step 1: Understand the concept of a circle through points
A circle can be defined by three points. If the three points are not collinear (i.e., they do not all lie on a single straight line), then exactly one circle can be drawn through them.
Step 2: Analyze the set of four points
Given four points P, Q, R, and S, we need to determine if we can draw a circle through all four points.
Step 3: Check for collinearity
If all four points are collinear, then no circle can be drawn through them. If any three of the four points are non-collinear, we can draw a circle through those three points. However, the fourth point may or may not lie on that circle.
Step 4: Conclusion on the number of circles
- If all four points are collinear, then 0 circles can be drawn.
- If any three points are non-collinear, then exactly 1 circle can be drawn through those three points, and the fourth point may not lie on that circle.
Thus, through any given set of four points, it is possible to draw at most 1 circle.
Final Answer:
At most 1 circle can be drawn through any given set of four points P, Q, R, and S.
---
A circle can be defined by three points. If the three points are not collinear (i.e., they do not all lie on a single straight line), then exactly one circle can be drawn through them.
Given four points P, Q, R, and S, we need to determine if we can draw a circle through all four points.
If all four points are collinear, then no circle can be drawn through them. If any three of the four points are non-collinear, we can draw a circle through those three points. However, the fourth point may or may not lie on that circle.
- If all four points are collinear, then 0 circles can be drawn.
- If any three points are non-collinear, then exactly 1 circle can be drawn through those three points, and the fourth point may not lie on that circle.
At most 1 circle can be drawn through any given set of four points P, Q, R, and S.
Topper's Solved these Questions
Similar Questions
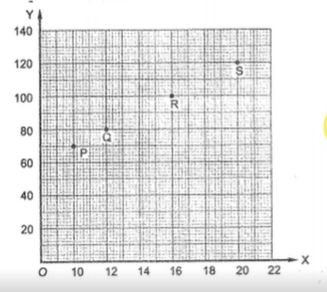
Find the coordinates of points P, Q, R and S in Figure.
View SolutionShow that the relation R on the set A of points in a plane, given by R={(P, Q): Distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further show that the set of all points related to a point P≠(0, 0) is the circle passing through P with origin as centre.
View Solution
Knowledge Check
TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
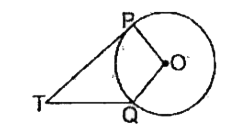 ANoBYesCCannot sayDData insufficient
ANoBYesCCannot sayDData insufficientA rectangular hyperbola whose centre is C is cut by any circle of radius r in four points P, Q, R and S. Then CP2+CQ2+CR2+CS2=
Ar2B2r2C3r2D4r2The length of four DNA fragments P, Q, R and s is such that P is smaller than Q, Q is smaller than 8 and R is greater than S. What would be position of the four given fragments on agarose gel from cathode to anode?
AR,S,Q,PBP,Q,R,SCR,Q,S,PDQ,P,S,R
Given four collinear points P, Q, R and S list all the line segments determined by them
View SolutionTo construct a line parallel to a given line and passing through a given point outside the line.
Question : Draw a line l, take a point P outside it. Draw a line m || line l passing through point P.
View SolutionFor any four points P,Q,R,S ∣∣¯¯¯¯¯¯PQׯ¯¯¯¯RS−bra(QR)ׯ¯¯¯¯PS+¯¯¯¯¯¯RPׯ¯¯¯¯¯QP∣∣ is equal to 4 times the are of the triangle .
View SolutionIn the following question, sentence has four portions marked P, Q, R and S. These four parts are not given in their proper order. Rearrange it in the proper sequence in order to make a meaningful sentence.
P. no cultured society is possible
Q. without books no fresh ideas are possible
R. and S. without fresh ideas
View SolutionWhich out of the four plant cells (P,Q,RandS) would not exhibit any wall pressure?

View Solution
