Three equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
6π(2+√3)2
π6(2+√3)2
π3(2+√3)2
3π(2+√3)2
The correct Answer is:C
Step by step video, text & image solution for Three equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionThree equal circles of radius unity touches one another. Radius of the circle touching all the three circles is:
View Solution
Knowledge Check
Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2If the four equal circles of radius 3 cm touch each other externally, then the area of the region bounded by the four circles is
A4(9−π) sq. cmB9(4−π) sq. cm.C5(6−π) sq. cm.D6(5−π) sq. cmThe radius of the circle circumscribing the triangle ABC, is equal to
A√102B√5C√10D√52
Three circles of equal radius 'a' cm touch each other. The area of the shaded region is :
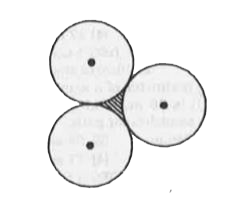
View SolutionThree circles of equal radius 'a' cm touch each other. The area of of the shaded region is :

View SolutionTwo circles of unit radius touch each other and each of them touches s internally touches a circle of radius two. Then the radius of the circle which touches all the three circles is :
View SolutionThe two circles touch each other if
View SolutionThree circles of radius a, b, c touch each other externally. The area of the triangle formed by joining their centre is
View Solution
