Question

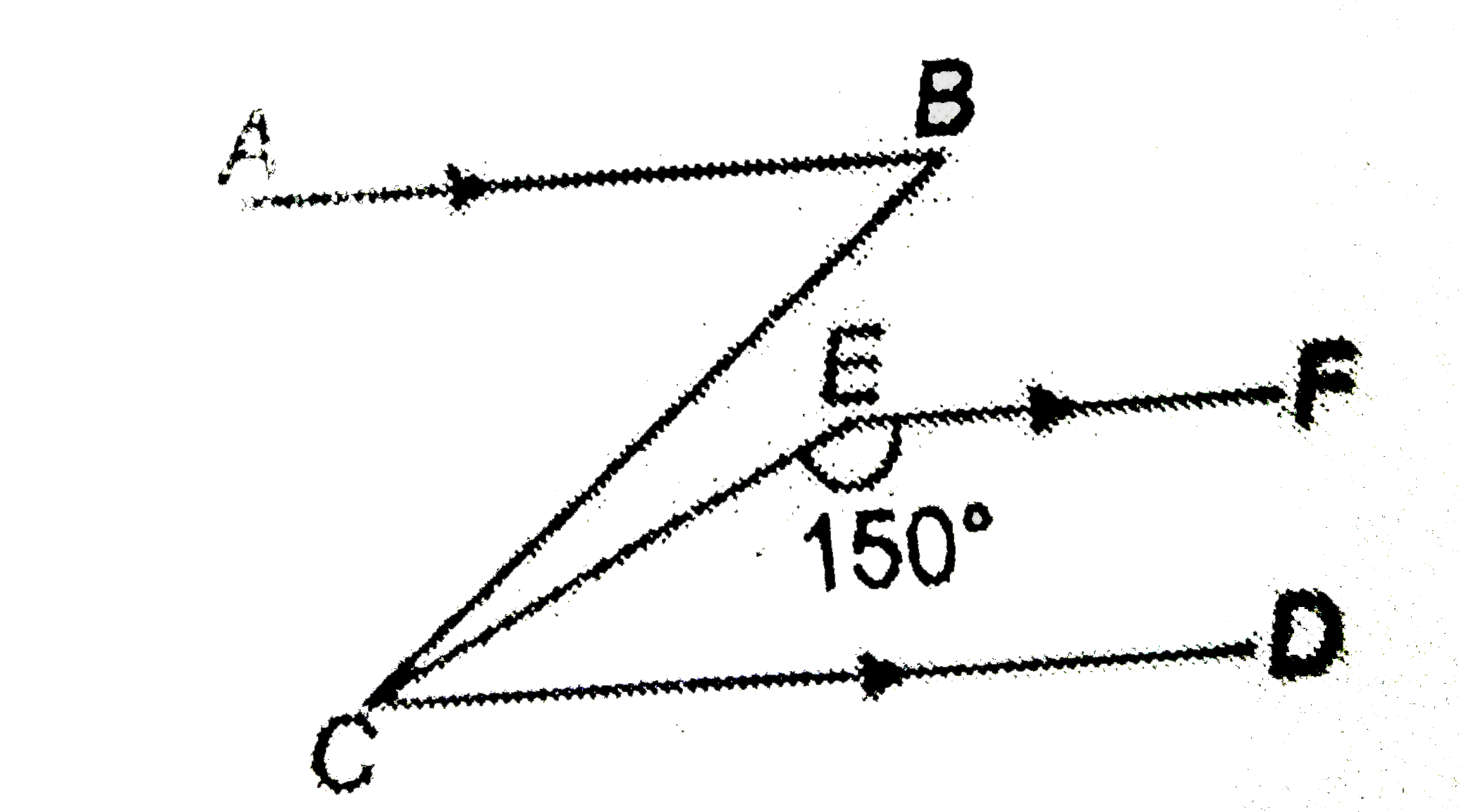
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of $\angle BEF$. If $\angle LEB={35}^{\circ }$ ,then $\angle CFQ$ will be :

Options

A. `70^@`
B. `55^@`
C. `110^@`
D. `125^@`

Answer

C

Explanation

To solve the problem, we need to analyze the given information step by step.

Step 1: Understand the Geometry
We have two parallel lines AB and CD, and a transversal line PQ that intersects AB at point E and CD at point F. The angle LEB is given as 35 degrees, and EL is the angle bisector of angle BEF.

Step 2: Identify Angles
Since EL is the bisector of angle BEF, we can denote:
- Angle LEB = 35 degrees (given)
- Angle LEF = 35 degrees (because EL bisects angle BEF)

Thus, angle BEF can be calculated as:
\( \text{Angle BEF} = \text{Angle LEB} + \text{Angle LEF} = 35^\circ + 35^\circ = 70^\circ \)

Step 3: Use the Properties of Parallel Lines
Since AB and CD are parallel lines, the angles formed by the transversal PQ have certain relationships. Specifically, the angles on the same side of the transversal (interior angles) sum up to 180 degrees.

Let’s denote:
- Angle EFD = x (the angle we need to find)

According to the property of parallel lines:
\( \text{Angle BEF} + \text{Angle EFD} = 180^\circ \)
Substituting the value of angle BEF:
\( 70^\circ + x = 180^\circ \)
Now, solve for x:
\( x = 180^\circ - 70^\circ = 110^\circ \)

Step 4: Find Angle CFQ
By the alternate interior angles theorem, angle CFQ is equal to angle EFD because they are corresponding angles formed by the transversal PQ with the parallel lines AB and CD.

Thus:
\( \text{Angle CFQ} = \text{Angle EFD} = 110^\circ \)

Final Answer
Therefore, the measure of angle CFQ is:
\( \text{Angle CFQ} = 110^\circ \)

---