Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
60∘
90∘
45∘
120∘
The correct Answer is:B
To solve the problem, we need to find the measure of angle MPN given the conditions of the parallel lines and the angle bisectors. Here's a step-by-step solution:
Step 1: Understand the Setup
We have two parallel lines AB and CD intersected by a transversal EF at points M and N. The lines MP and NP are the angle bisectors of angles BMN and DNM, respectively.
Step 2: Identify Angles
Let:
- Angle BMN = x
- Angle DNM = y
Since AB is parallel to CD, we know that:
- Angle BMN + Angle DNM = 180° (because they are corresponding angles formed by the transversal EF).
Step 3: Set Up the Equation
From the above relationship, we can write:
x+y=180°
Step 4: Use the Angle Bisector Property
Since MP is the bisector of angle BMN, it divides angle BMN into two equal parts:
Angle BMP=x2
Angle PMN=x2
Similarly, since NP is the bisector of angle DNM:
Angle DNP=y2
Angle MNP=y2
Step 5: Find Angle MPN
Now, we need to find angle MPN. In triangle MPN, the sum of the angles is 180°:
Angle MPN+Angle PMN+Angle MNP=180°
Substituting the values we have:
Angle MPN+x2+y2=180°
Step 6: Simplify the Equation
Now, we can simplify this equation:
Angle MPN+x+y2=180°
Since we know from Step 3 that x+y=180°, we can substitute this into our equation:
Angle MPN+180°2=180°
Angle MPN+90°=180°
Step 7: Solve for Angle MPN
Now, solving for angle MPN:
Angle MPN=180°−90°=90°
Thus, the measure of angle MPN is:
Angle MPN=90°
Final Answer
Angle MPN is equal to 90°.
---
We have two parallel lines AB and CD intersected by a transversal EF at points M and N. The lines MP and NP are the angle bisectors of angles BMN and DNM, respectively.
Let:
- Angle BMN = x
- Angle DNM = y
- Angle BMN + Angle DNM = 180° (because they are corresponding angles formed by the transversal EF).
From the above relationship, we can write:
x+y=180°
Since MP is the bisector of angle BMN, it divides angle BMN into two equal parts:
Angle BMP=x2
Angle PMN=x2
Angle DNP=y2
Angle MNP=y2
Now, we need to find angle MPN. In triangle MPN, the sum of the angles is 180°:
Angle MPN+Angle PMN+Angle MNP=180°
Angle MPN+x2+y2=180°
Now, we can simplify this equation:
Angle MPN+x+y2=180°
Angle MPN+180°2=180°
Angle MPN+90°=180°
Now, solving for angle MPN:
Angle MPN=180°−90°=90°
Angle MPN=90°
Angle MPN is equal to 90°.
Topper's Solved these Questions
Similar Questions
Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View Solution
Knowledge Check
Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘Two parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘Dnone of theseTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘DNone of these
If two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
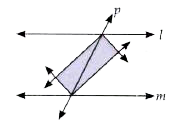
View SolutionAB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :

View SolutionIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View Solution
