Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
60∘
90∘
45∘
120∘
The correct Answer is:B
Step by step video, text & image solution for Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively. The lines MP and NP are the bisectors of interior angles angle BMN and angle DNM on the same side of the transversal. Then angle MPN is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.3
28 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - Fast Track Practice
104 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View Solution
Knowledge Check
Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘Two parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘Dnone of theseTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
A180∘B60∘C90∘DNone of these
If two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
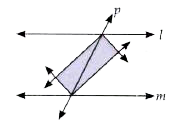
View SolutionAB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :

View SolutionIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View Solution
