AB and CD are two parallel lines, PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ then ∠CFQ will be :
70∘
55∘
110∘
125∘
The correct Answer is:C
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Given Information
We have two parallel lines AB and CD, and a transversal PQ that intersects these lines at points E and F respectively. The angle bisector EL divides angle BEF into two equal parts. We know that angle LEB = 35°.
Hint: Identify the relationships between the angles formed by the transversal and the parallel lines.
Step 2: Determine Angle LEF
Since EL is the angle bisector of angle BEF, we can conclude that angle LEF is also equal to angle LEB. Therefore, angle LEF = 35°.
Hint: Remember that an angle bisector divides an angle into two equal parts.
Step 3: Calculate Angle BEF
Now, we can find angle BEF. Since angle BEF is composed of angle LEB and angle LEF:
Angle BEF=Angle LEB+Angle LEF=35°+35°=70°.
Hint: Use the property of angle bisectors to find the total angle.
Step 4: Use the Parallel Lines Property
Since AB and CD are parallel lines, angle BEF is equal to angle CFE (by the Alternate Interior Angles Theorem). Therefore:
Angle CFE=Angle BEF=70°.
Hint: Recall that alternate interior angles are equal when two lines are parallel.
Step 5: Set Up the Equation for Straight Line PQ
Since PQ is a straight line, the sum of angles CFE and CFQ must equal 180°:
Angle CFE+Angle CFQ=180°.
Hint: Remember that the angles on a straight line sum up to 180°.
Step 6: Solve for Angle CFQ
Substituting the known value of angle CFE into the equation:
70°+Angle CFQ=180°.
Now, isolate angle CFQ:
Angle CFQ=180°−70°=110°.
Hint: Perform simple arithmetic to find the unknown angle.
Conclusion
Thus, the measure of angle CFQ is 110°.
Final Answer: Angle CFQ = 110°.
We have two parallel lines AB and CD, and a transversal PQ that intersects these lines at points E and F respectively. The angle bisector EL divides angle BEF into two equal parts. We know that angle LEB = 35°.
Since EL is the angle bisector of angle BEF, we can conclude that angle LEF is also equal to angle LEB. Therefore, angle LEF = 35°.
Now, we can find angle BEF. Since angle BEF is composed of angle LEB and angle LEF:
Angle BEF=Angle LEB+Angle LEF=35°+35°=70°.
Since AB and CD are parallel lines, angle BEF is equal to angle CFE (by the Alternate Interior Angles Theorem). Therefore:
Angle CFE=Angle BEF=70°.
Since PQ is a straight line, the sum of angles CFE and CFQ must equal 180°:
Angle CFE+Angle CFQ=180°.
Substituting the known value of angle CFE into the equation:
70°+Angle CFQ=180°.
Now, isolate angle CFQ:
Angle CFQ=180°−70°=110°.
Thus, the measure of angle CFQ is 110°.
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.2
Explore 100 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.3
Explore 28 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:Fast Track Practice
Explore 104 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ ,then ∠CFQ will be :
A70∘B55∘C110∘D125∘AB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :
 ArectangleBsquareCparallelogramDnone of these
ArectangleBsquareCparallelogramDnone of theseTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
AB and CD are two parallel lines and a transversal 'l' intersects these lines at X and Y respectively Prove that the bisectors of interior angles from a parallelogram whose each angle is 90∘.
View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EP and FQ are the bisectors of ∠AEF and ∠EFD respectively, prove that EP∣∣FQ.

View SolutionAB and CD are parallel straight lines. EG intersects the lines AB and CD at F and G respectively. If ∠AFE=60∘ and the straight line HI bisects ∠EGD, then ∠DGI is
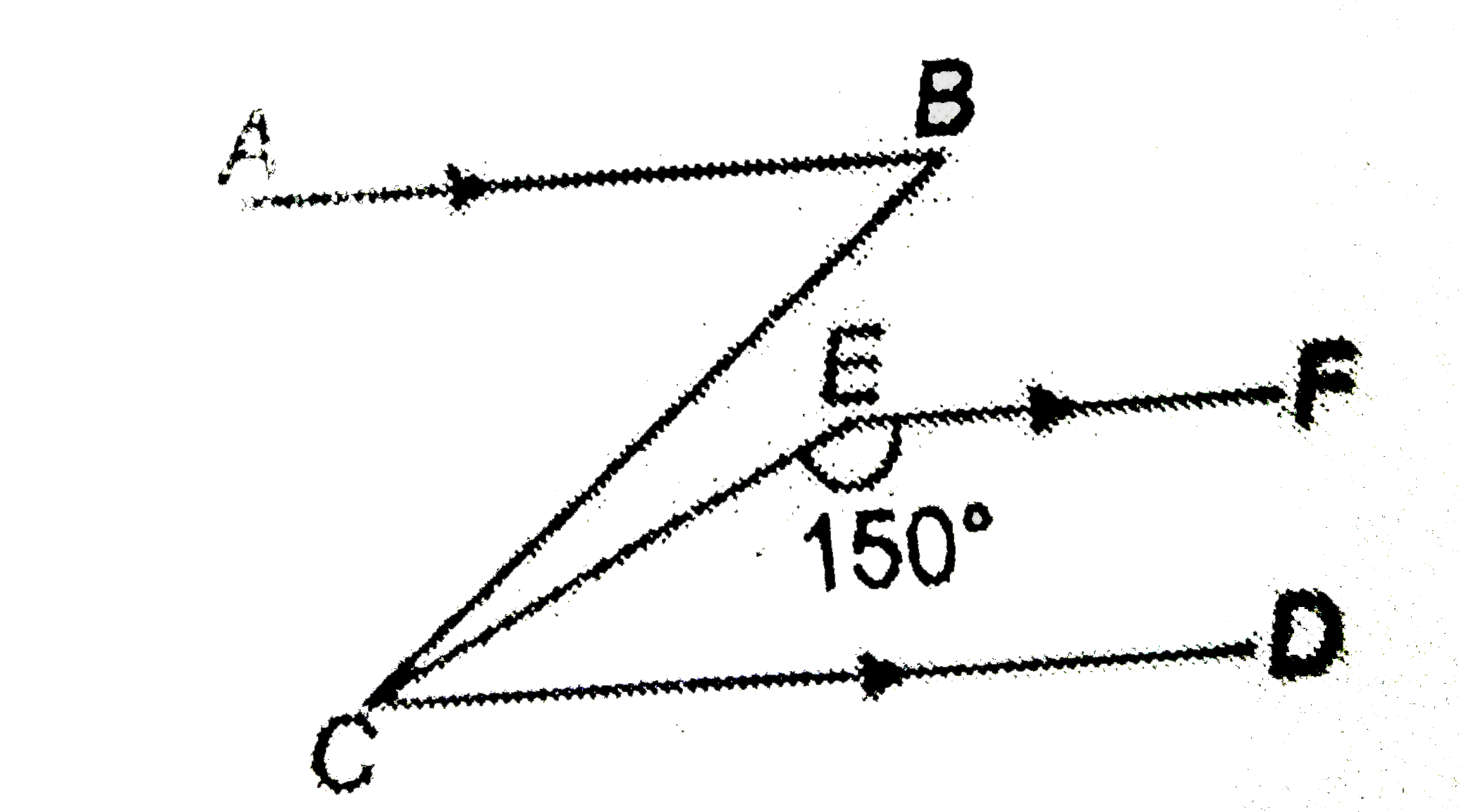
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
View SolutionTwo parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :
View Solution