AB and CD are intersecting lines. OD is bisector of ∠BOY. Find x.
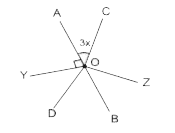
The correct Answer is:x=15∘
Step by step video, text & image solution for AB and CD are intersecting lines. OD is bisector of angleBOY. Find x. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINES AND ANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-D
8 Videos
- LINES AND ANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PRACTICE TEST
8 Videos
- LINES AND ANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-B
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - PRACTICE TEST
12 Videos
- NUMBER SYSTEMSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NUMBER SYSTEMSEXERCISE - Part - D
18 Videos
Similar Questions
The line segments AB and CD intersect at O. OF is the internal bisector of obtuse angle BOC and OE is the internal bisector of acute angle AOC. If ∠BOC=130∘, what is the measure of ∠FOE?
View SolutionIn the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
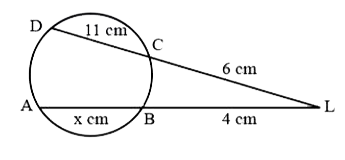
View Solution
Knowledge Check
AB and CD are two parallel lines, PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ then ∠CFQ will be :
A70∘B55∘C110∘D125∘AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ ,then ∠CFQ will be :
A70∘B55∘C110∘D125∘The straight lines AB and CD intersect at E . If EF and EG are bisectors of ∠DEAand∠AEC respectively and if ∠AEF=xand∠AEG=y , then
Ax+y>.90∘Bx+y<90∘Cx+y=90∘Dx+y=180∘
In the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View SolutionAB and CD are parallel straight lines. EG intersects the lines AB and CD at F and G respectively. If ∠AFE=60∘ and the straight line HI bisects ∠EGD, then ∠DGI is
View SolutionABCD is a parallelogram. The bisector of angle A intersects CD at X and bisector of angle C intersects AB at Y. Is AXCY a parallelogram? Give reason.
View SolutionTwo lines AB and CD intersect at a point O such that ∠BOC+∠AOD=280∘, as shown in the figure. Find all the four angles.
View SolutionAB and CD are two parallel lines and a transversal PO intersects AB and CD at M and N respectively. The bisector of the interior angles form a quadrilateral :
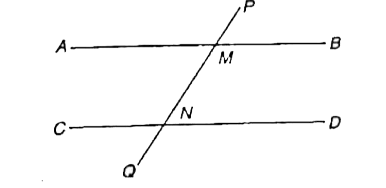
View Solution
