A horizontal board is oscillating with an amplitude of 3 m. If the frequency of oscillation is 15 per minute, find the minimum value of coefficient of friction in order that a body placed on the board will A not slide when the board oscillates ?
The correct Answer is:0.75
To solve the problem, we need to find the minimum value of the coefficient of friction (μ) that prevents a body from sliding on a horizontally oscillating board. Here’s a step-by-step solution:
Step 1: Understand the given parameters
- Amplitude (A) = 3 m
- Frequency (f) = 15 per minute = 15/60 Hz = 0.25 Hz
Step 2: Convert frequency to angular frequency (ω)
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×0.25=π2 rad/s
Step 3: Calculate the maximum acceleration (a_max)
The maximum acceleration (a_max) of the oscillating board can be calculated using the formula:
amax=Aω2
Substituting the values of A and ω:
amax=3×(π2)2=3×π24
Calculating this:
amax≈3×2.467=7.401 m/s2
Step 4: Set up the equation for friction
For the body to not slide, the frictional force must be equal to or greater than the pseudo force acting on the body due to the maximum acceleration. The pseudo force is given by:
Fpseudo=m⋅amax
The frictional force (F_friction) is given by:
Ffriction=μmg
Setting these two forces equal for the condition of no sliding:
μmg=mamax
Step 5: Simplify the equation
We can cancel the mass (m) from both sides:
μg=amax
Thus, we can express μ as:
μ=amaxg
Step 6: Substitute the values to find μ
Using g≈10 m/s2:
μ=7.40110≈0.7401
Step 7: Final answer
The minimum value of the coefficient of friction (μ) required to prevent the body from sliding is approximately:
μ≈0.74
- Amplitude (A) = 3 m
- Frequency (f) = 15 per minute = 15/60 Hz = 0.25 Hz
The angular frequency (ω) is given by the formula:
ω=2πf
Substituting the value of f:
ω=2π×0.25=π2 rad/s
The maximum acceleration (a_max) of the oscillating board can be calculated using the formula:
amax=Aω2
Substituting the values of A and ω:
amax=3×(π2)2=3×π24
Calculating this:
amax≈3×2.467=7.401 m/s2
For the body to not slide, the frictional force must be equal to or greater than the pseudo force acting on the body due to the maximum acceleration. The pseudo force is given by:
Fpseudo=m⋅amax
The frictional force (F_friction) is given by:
Ffriction=μmg
Setting these two forces equal for the condition of no sliding:
μmg=mamax
We can cancel the mass (m) from both sides:
μg=amax
Thus, we can express μ as:
μ=amaxg
Using g≈10 m/s2:
μ=7.40110≈0.7401
The minimum value of the coefficient of friction (μ) required to prevent the body from sliding is approximately:
μ≈0.74
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM TIME PERIOD OF OSCILLATION OF A S.H. OSCILLATOR)
19 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
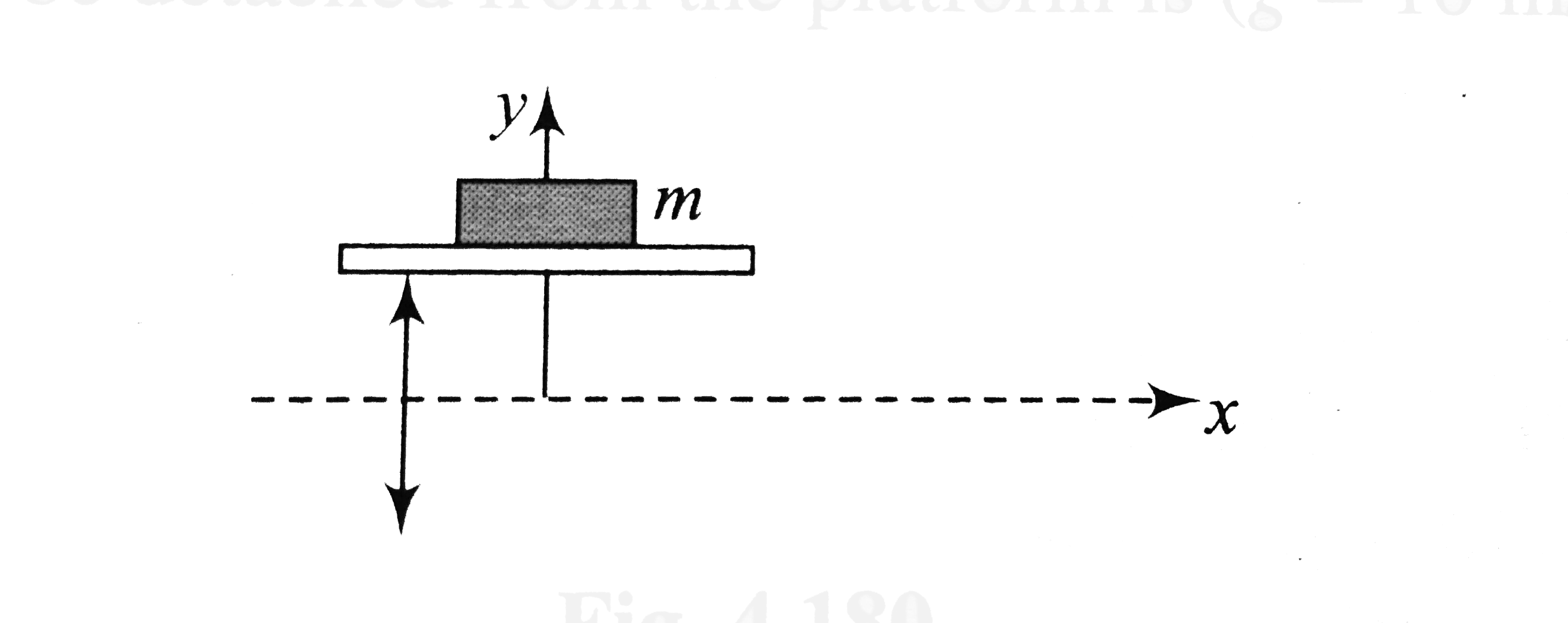
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
View SolutionA plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s.
View Solution
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
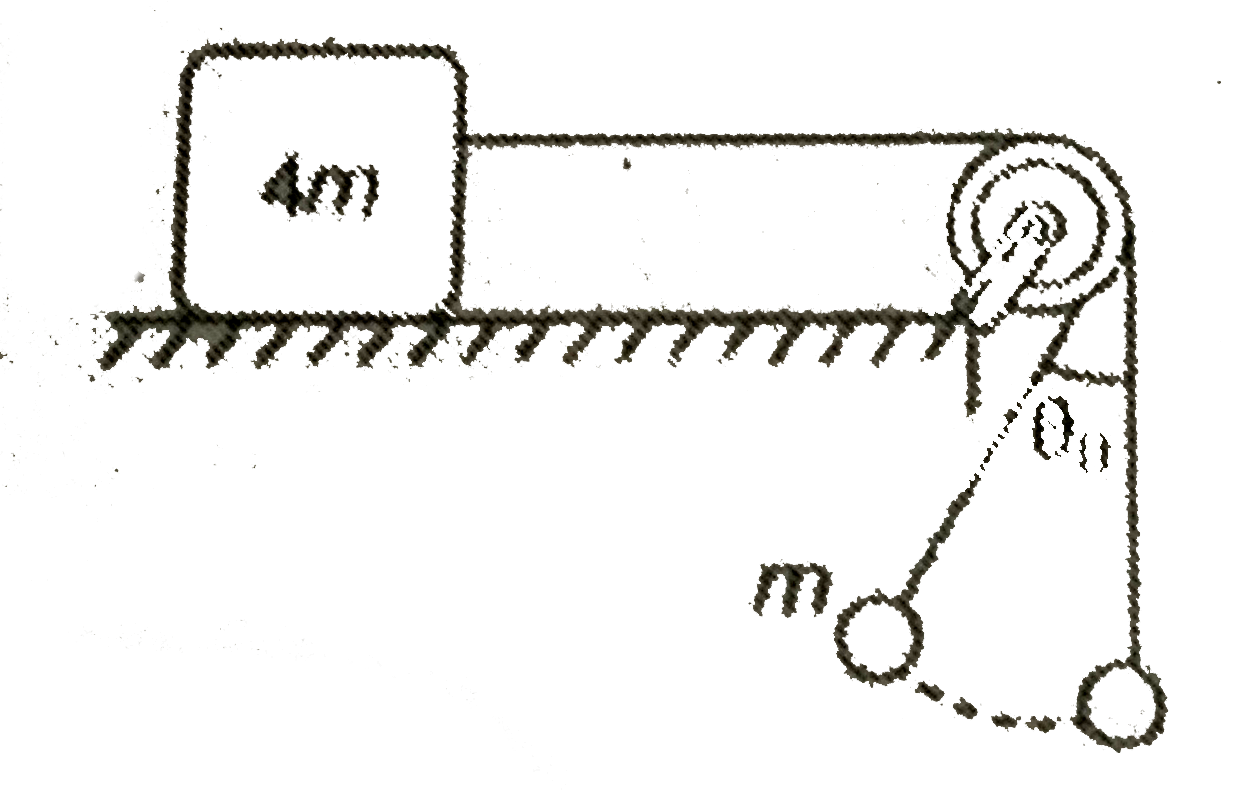
View SolutionTwo bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)

View SolutionTwo bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)

View SolutionA cubical block of mass M and side a is placed on a rough horizontal plane as shown in the figure A force F is acting on the block at height3a4 from the bottom. The minimum value of coefficient of friction (μ) such that block lopples without sliding will be
View SolutionA block rests on a horizontal table which is executing SHM in the horizontal plane with an amplitude A. What will be the frequency of oscillation, the block will just start to slip? Coefficient of friction=μ.
View SolutionA body executing shm completes 120 oscillations per minute. If the amplitude of oscillations is 6 cm, find the velocity and acceleration of the particle when it is at a distance of 4 cm from the mean position?
View SolutionTwo bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
View SolutionA body A mass m1=1kg and body B of mass m2=4.1kg. The body A perform free vertical harmonic oscillations with the amplitude 1.6cm and frequency 25Hz. Neglecting the mass of the spring , find the maximum and m inimum value of force that the system exerts on the hearing surface.

View Solution
