A block rests on a horizontal table which is executing SHM in the horizontal plane with an amplitude A. What will be the frequency of oscillation, the block will just start to slip? Coefficient of friction.
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the block and relate them to the frequency of oscillation of the table.
Step 1: Understand the forces acting on the block
The block is resting on a table that is executing simple harmonic motion (SHM). The key forces acting on the block are:
- The gravitational force (weight) acting downwards, which is mg.
- The normal force N acting upwards, which balances the weight of the block in the vertical direction.
- The frictional force that prevents the block from slipping, which is given by Ff=μN.
Since there are no vertical accelerations, we have:
N=mg
Step 2: Determine the maximum acceleration of the table
The table is executing SHM with an amplitude A. The maximum acceleration amax of the table can be expressed as:
amax=ω2A
where ω is the angular frequency of the SHM.
Step 3: Relate the maximum acceleration to the frictional force
For the block to just start slipping, the maximum frictional force must equal the net force acting on the block due to the acceleration of the table. The maximum frictional force is:
Ff=μN=μmg
Setting the maximum frictional force equal to the force due to the maximum acceleration:
μmg=mamax
Substituting for amax:
μmg=mω2A
Step 4: Simplify the equation
We can cancel m from both sides (assuming m≠0):
μg=ω2A
Step 5: Solve for the angular frequency ω
Rearranging the equation gives:
ω2=μgA
Taking the square root of both sides:
ω=√μgA
Step 6: Convert angular frequency to frequency
The frequency f is related to angular frequency ω by the formula:
f=ω2π
Substituting for ω:
f=12π√μgA
Final Answer
Thus, the frequency of oscillation at which the block will just start to slip is:
f=12π√μgA
The block is resting on a table that is executing simple harmonic motion (SHM). The key forces acting on the block are:
- The gravitational force (weight) acting downwards, which is mg.
- The normal force N acting upwards, which balances the weight of the block in the vertical direction.
- The frictional force that prevents the block from slipping, which is given by Ff=μN.
N=mg
The table is executing SHM with an amplitude A. The maximum acceleration amax of the table can be expressed as:
amax=ω2A
where ω is the angular frequency of the SHM.
For the block to just start slipping, the maximum frictional force must equal the net force acting on the block due to the acceleration of the table. The maximum frictional force is:
Ff=μN=μmg
μmg=mamax
Substituting for amax:
μmg=mω2A
We can cancel m from both sides (assuming m≠0):
μg=ω2A
Rearranging the equation gives:
ω2=μgA
Taking the square root of both sides:
ω=√μgA
The frequency f is related to angular frequency ω by the formula:
f=ω2π
Substituting for ω:
f=12π√μgA
Thus, the frequency of oscillation at which the block will just start to slip is:
f=12π√μgA
Similar Questions
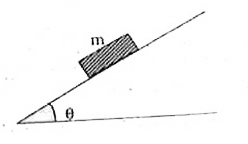
In the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
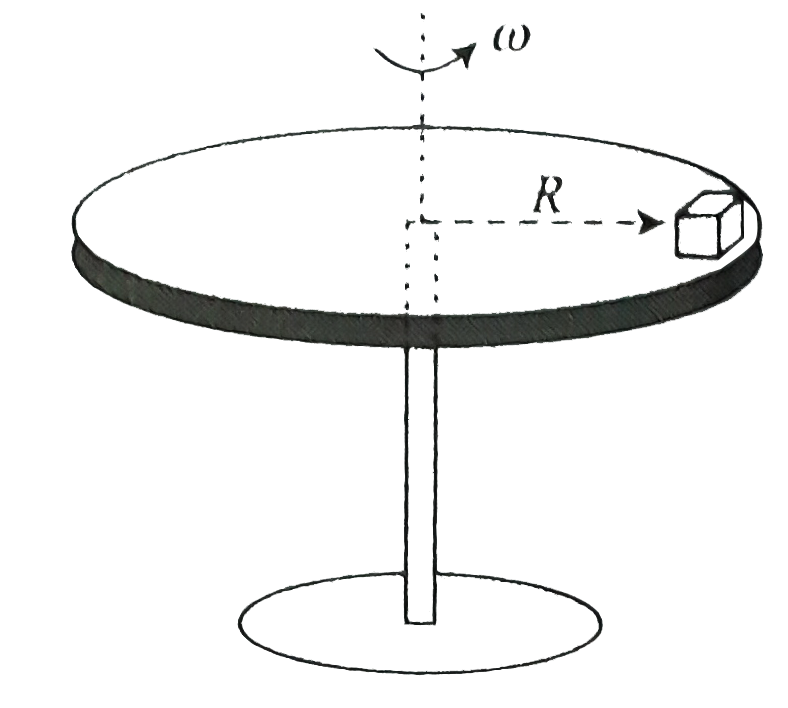
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA block is on horizontal slab which is moving horizontally and excuting S.H.M. The coefficient of static frication between block and slab is μ. If block is not separated from slab then determine range of angular frequency of oscillation.
View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA mass of 2kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=20∘ with the horizontal, the mass just begins to slides. What is the coefficient of static friction between the block and the surface ?
View SolutionA block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA small block is kept on a platform executing SHM in the horizontal plane, described by x=Asinωt. The time period of SHM is T and the coefficient of friction between the block and the platform is μ. The condition that the block does not slip on the platform at any instant is μ≥xπ2AgT2 then write the value of 'x'

View SolutionA block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friciton between block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface.
View Solution
