A block is kept on a horizontal table that is executing simple harmonic motion of frequency v in the horizontal plane. The coefficient of static friction between the block and the table is μ. Determine the maximum amplitude of the table for which the block does not slip on the surface of the table.
To solve the problem of determining the maximum amplitude of the table for which the block does not slip on the surface of the table, we can follow these steps:
1. Understand the Forces Acting on the Block:
- The block experiences a frictional force due to the table's motion. This frictional force is what prevents the block from slipping off the table.
2. Identify the Maximum Frictional Force:
- The maximum static friction force Fmax that can act on the block is given by:
Fmax=μmg
where μ is the coefficient of static friction, m is the mass of the block, and g is the acceleration due to gravity.
3. Relate Friction to Acceleration:
- The maximum acceleration amax that the block can experience without slipping is given by:
amax=Fmaxm=μg
4. Determine the Maximum Acceleration of the Table:
- The table is executing simple harmonic motion (SHM). The maximum acceleration atable of the table is related to its amplitude A and angular frequency ω as follows:
atable=Aω2
where ω=2πv (with v being the frequency of the SHM).
5. Set the Maximum Accelerations Equal:
- For the block to not slip, the maximum acceleration of the table must not exceed the maximum acceleration of the block:
Aω2≤μg
6. Substitute for Angular Frequency:
- Substitute ω=2πv into the equation:
A(2πv)2≤μg
7. Solve for the Maximum Amplitude A:
- Rearranging the equation gives:
A≤μg(2πv)2
- Therefore, the maximum amplitude Amax is:
Amax=μg4π2v2
Final Answer:
The maximum amplitude of the table for which the block does not slip on the surface of the table is:
Amax=μg4π2v2
- The block experiences a frictional force due to the table's motion. This frictional force is what prevents the block from slipping off the table.
- The maximum static friction force Fmax that can act on the block is given by:
Fmax=μmg
where μ is the coefficient of static friction, m is the mass of the block, and g is the acceleration due to gravity.
- The maximum acceleration amax that the block can experience without slipping is given by:
amax=Fmaxm=μg
- The table is executing simple harmonic motion (SHM). The maximum acceleration atable of the table is related to its amplitude A and angular frequency ω as follows:
atable=Aω2
where ω=2πv (with v being the frequency of the SHM).
- For the block to not slip, the maximum acceleration of the table must not exceed the maximum acceleration of the block:
Aω2≤μg
- Substitute ω=2πv into the equation:
A(2πv)2≤μg
- Rearranging the equation gives:
A≤μg(2πv)2
- Therefore, the maximum amplitude Amax is:
Amax=μg4π2v2
The maximum amplitude of the table for which the block does not slip on the surface of the table is:
Amax=μg4π2v2
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Very Short Answer Questions)
37 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Additional Question )
3 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question ( short Answer Type Questions )
6 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA block is kept on a horizontal table. The stable is undergoing simple harmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friciton between block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface.
View Solution
Knowledge Check
The system shown is just on the verge of slipping. The coefficient of static friction between the block and the table top is :
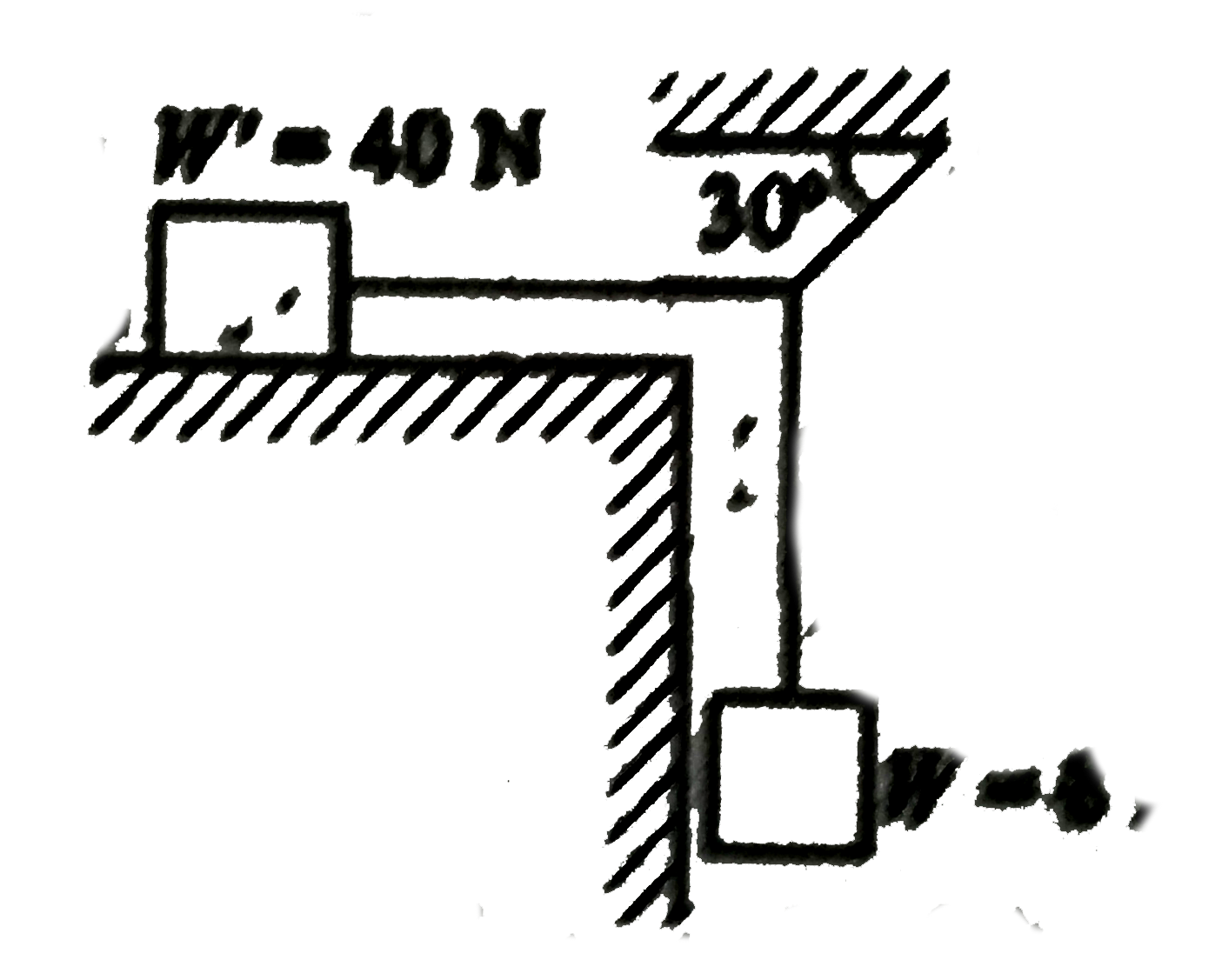 A0.5B0.95C0.15D0.35
A0.5B0.95C0.15D0.35A block on a horizontal slab is moving horizontally with a simple harmonic motion of frequency two oscillations per second. If the coefficient of static friction between block and slab is 0.5, then the amplitude of the oscillation will be (if the block does not slip along the slab)
A3.3 cmB3.5 cmC3.15 cmD7 cmA block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
ABy the applied force is 150 JBBy the frictional force is 60 JCBy the applied force and the net force are 150 J and 90 J respectivelyDAll are correct
A block is on a horizontal surface (a shake table) that is moving back and forth horizontally with simple harmonic motion of frequency 2.0 Hz. The coefficient of static friction between block and surface is 0.45. How great can the amplitude of the SHM be if the block is not to slip along the surface?
View SolutionThe coefficient of friction between the block and the wedge is μ. Friction between the wedge and the table is to be neglected.
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionThe coefficient of friction between the wedge and the table is μ. Friction between the block and the wedge is to be neglected.
View Solution
