The figure shows an arrangement of mass m with three springs of different springs constant. When m is slightly displaced and then released, find the frequency of its motion.
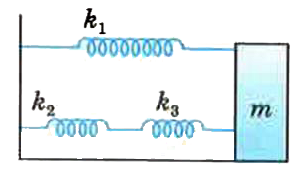
Here, two springs of force constans k2andk3 are in series and the third spring of force constant k1 is in parallel with their series combination. Therefore, equivalent force constant of the arrangement is
k.=k2k3k2+k3+k1
The time period is given by
T=2π√mk.=2π
⎷mk2k3k2+k3+k1
or T=2π√m(k2+k3)k2k3+k3k1+k3k2
Frequency, v=1T
v=12π√k2k3+k3k1+k1k2m(k2+k3)
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Revision Exercises (Very Short Answer Questions)
Explore 37 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Revision Exercises (Additional Question )
Explore 3 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:NCERT Exemplar Problems Subjective Question ( short Answer Type Questions )
Explore 6 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
The figure shows the arrangement of three springs of different spring constant, connected to a mass m. When mass m oscillates find equivalent spring constant and the time period of vibration.
View SolutionIn the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
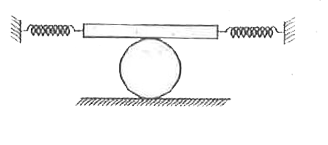
View Solution
Knowledge Check
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
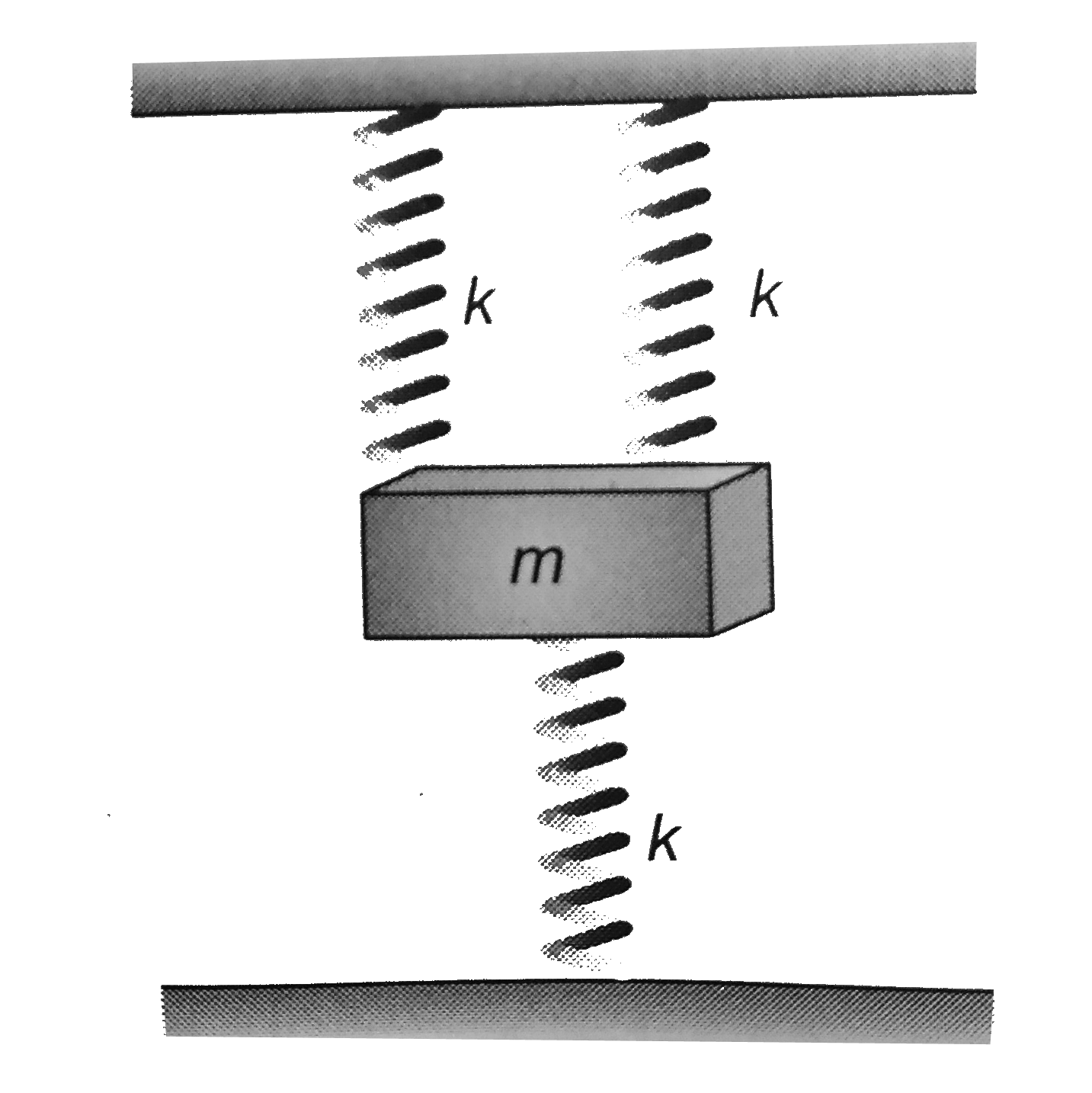
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4In the figure all spring are identical having spring constant k and mass m each .The block hav also mass m .The frequency of oscillation of the block is
 A12π√3kmB12π√3k2mC2π√3m3kDNone of these
A12π√3kmB12π√3k2mC2π√3m3kDNone of these
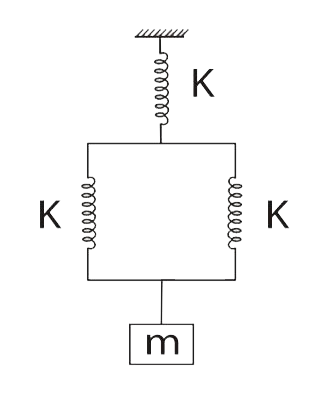
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

View Solutionfour different springs arrangements. If the mass m in each arrangement is displaced from its equilibrium position and released, what is the resulting frequency of vibration ini each case? Neglect the mass of the spring. Figure (a) and (b) represent an arrangement of springs in parallel and (c) and (d) represent springs in series?

View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
View Solution

