A small lead sphere is made to execute shm inside a concave dish of radius of curvature 1 m. What is its period ?
The correct Answer is:2 second
To find the period of a small lead sphere executing simple harmonic motion (SHM) inside a concave dish of radius of curvature 1 m, we can follow these steps:
1. Understand the Problem: We have a small lead sphere inside a concave dish. The dish has a radius of curvature R=1m. We need to find the time period T of the SHM.
2. Identify the Formula: The time period T for a small object executing SHM in a concave dish can be expressed using the formula:
T=2π√R−rg
where:
- R is the radius of the dish,
- r is the radius of the sphere,
- g is the acceleration due to gravity (approximately 9.8m/s2).
3. Approximation for Small Sphere: Since the sphere is described as "small," we can approximate R−r as R (because r is much smaller than R):
R−r≈R
4. Substitute Values into the Formula: Now substituting R=1m and g=9.8m/s2:
T=2π√19.8
5. Calculate the Square Root: First, calculate the square root:
√19.8≈√0.10204≈0.319
6. Calculate the Time Period: Now, substitute back into the equation for T:
T=2π×0.319≈2×3.14×0.319≈2.006≈2seconds
Final Answer:
The period of the small lead sphere executing SHM inside the concave dish is approximately 2seconds.
T=2π√R−rg
where:
- R is the radius of the dish,
- r is the radius of the sphere,
- g is the acceleration due to gravity (approximately 9.8m/s2).
R−r≈R
T=2π√19.8
√19.8≈√0.10204≈0.319
T=2π×0.319≈2×3.14×0.319≈2.006≈2seconds
The period of the small lead sphere executing SHM inside the concave dish is approximately 2seconds.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM TIME PERIOD OF OSCILLATION OF A S.H. OSCILLATOR)
19 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
What is the focal length of a concave mirror of radius of curvature 16.0 cm?
View SolutionThe radius of a sphere is 1.23 cm. What is its surface area?
View SolutionA sphere of radius r is kept on a concave mirror of radius of curation R. The arrangement is kept on a horizontal surface (the surface of concave mirror is friction less and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
View SolutionA thin plano-convex lens acts like a concave mirror of radius of curvature 20cm when its plane surface is silvered. The radius of curvature of the curved surface if index of refraction of its matarial is 1.5 will be
View SolutionA thin plano-convex lens acts like a concave mirror of radius of curvature 20cm when its plane surface is silvered. The radius of curvature of the curved surface if index of refraction of its matarial is 1.5 will be
View SolutionThe focal length of a concave mirror is 10 cm. Find its radius of curvature.
View SolutionAn object of height 1mm is placed inside a sphere of refractive index μ=2 and radius of curvature 20 cm as shown in the figure. Find the position, size, and nature of image, for the situation shown in Figure. Draw ray diagram.
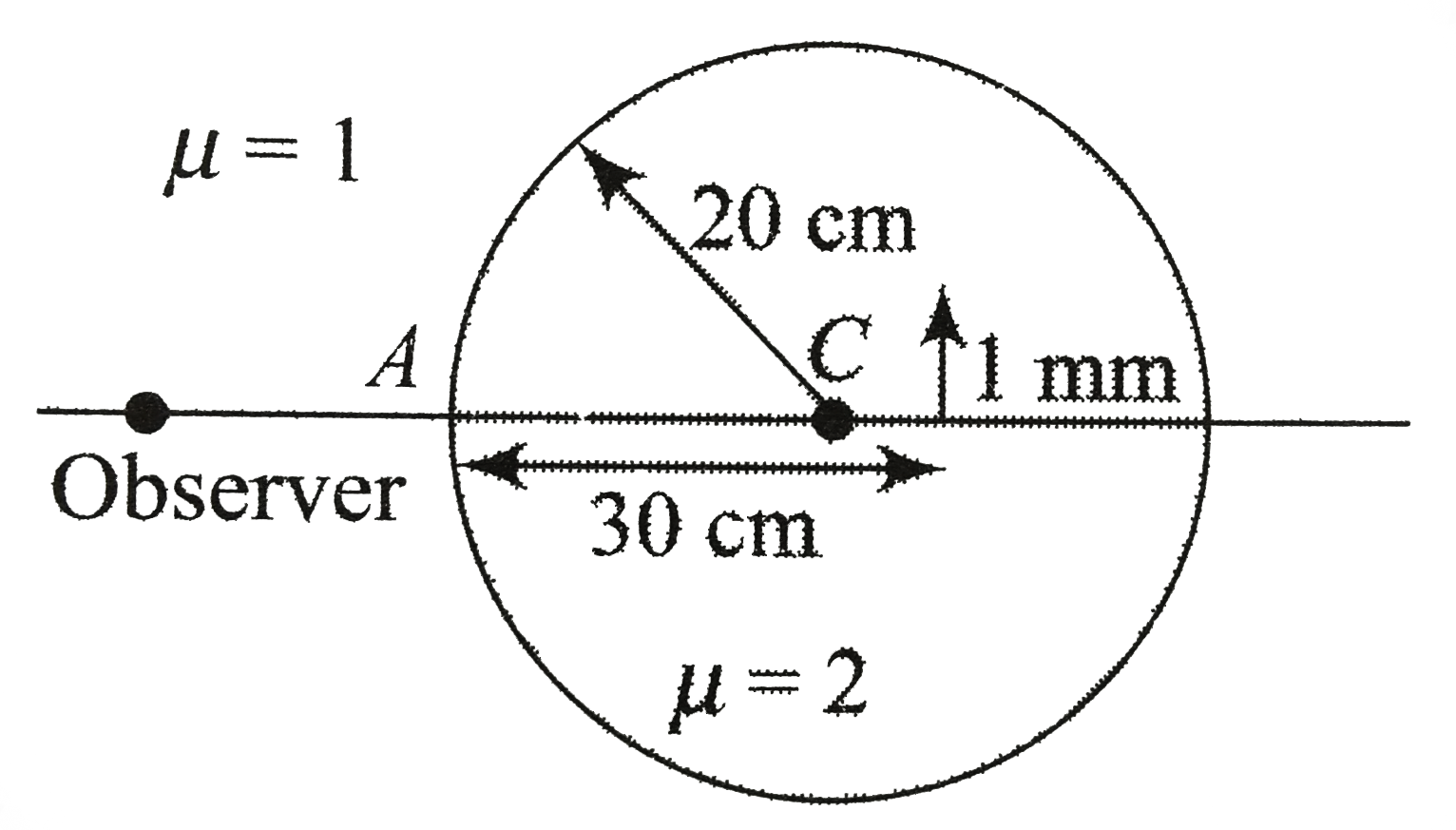
View SolutionA plano-concave lens is made of glass of refractive index 1.5 and the radius of curvature of its curved face is 100 cm. What is the power of the lens?
View SolutionSuppose the bob in a simple pendulum is a hollow sphere with a small hole at the bottom. The sphere is filled with water and is made to oscillate. What happens to the period ?
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View Solution
