If two springs of force constants are connected in series and is fixed to a body of mass 100 g. Find the period of oscillation.
The correct Answer is:1 second
To solve the problem of finding the period of oscillation for a mass connected to two springs in series, we can follow these steps:
Step 1: Identify the given values
We have two springs with force constants:
- k1=7N/m
- k2=9N/m
The mass attached to the springs is:
- m=100g=0.1kg (since 1 kg = 1000 g)
Step 2: Calculate the equivalent spring constant
For springs connected in series, the equivalent spring constant keq can be calculated using the formula:
1keq=1k1+1k2
Substituting the values:
1keq=17+19
To add these fractions, we find a common denominator. The least common multiple of 7 and 9 is 63:
1keq=963+763=1663
Now, taking the reciprocal to find keq:
keq=6316N/m
Step 3: Calculate the period of oscillation
The period T of oscillation for a mass-spring system is given by the formula:
T=2π√mkeq
Substituting the values:
T=2π
⎷0.16316
This simplifies to:
T=2π√0.1×1663=2π√1.663
Calculating the square root:
T=2π√0.0253968253968254≈2π×0.159
Now calculating T:
T≈0.997s≈1s
Final Answer:
The period of oscillation is approximately 1s.
---
We have two springs with force constants:
- k1=7N/m
- k2=9N/m
- m=100g=0.1kg (since 1 kg = 1000 g)
For springs connected in series, the equivalent spring constant keq can be calculated using the formula:
1keq=1k1+1k2
1keq=17+19
1keq=963+763=1663
keq=6316N/m
The period T of oscillation for a mass-spring system is given by the formula:
T=2π√mkeq
T=2π
⎷0.16316
T=2π√0.1×1663=2π√1.663
T=2π√0.0253968253968254≈2π×0.159
T≈0.997s≈1s
The period of oscillation is approximately 1s.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (PERIOD OF OSCILLATION OF (i) A LIQUID IN A U-TUBE, (ii) TEST TUBE FLOAT, (iii) (iii) A PISTON IN AN ENGINE etc.)
9 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (FROM ENERGY OF AS.H. OSCILLATOR )
9 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Two springs of force constants 7Nm−1and9Nm−1 are connected in parallel and is fixed to body of mass 100 g. Find the period of oscillation.
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionTwo springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
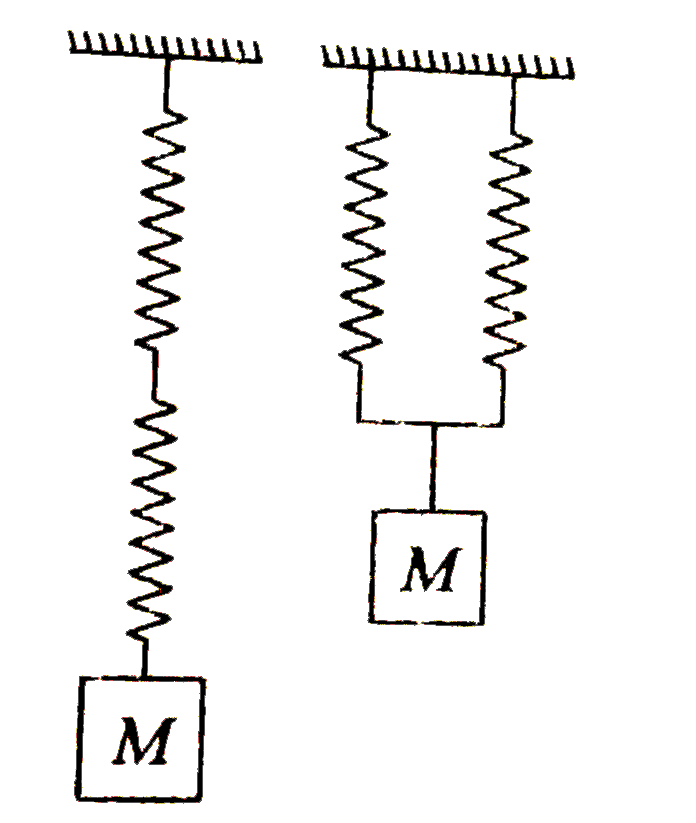
View SolutionA particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is
View SolutionTwo rigid bodies A and B of masses 1 kg and 2 kg respectively are rigidly connected to a spring of force constant 400 Nm−1 . The body B rests on a horizontal table. From the rest position , the body A is compressed by 2 cm and then released . Deduce (i) teh frequency of oscillation, (ii) total oscillation energy, (iii) the amplitude of the harmonic vibration of the reaction of the table on body B.

View Solution
