An impulsive force gives an initial velocity of −1.0ms−1 to the mass in the unstretched spring position. What is the amplitude of motion ? Give x as a function of time for the oscillating mass. Given m=3 kg, k=1200Nm−1
The correct Answer is:(1/20)m
To solve the problem, we need to determine the amplitude of motion and express the position x as a function of time for a mass-spring system. Given the mass m=3kg and spring constant k=1200N/m, we start with the initial conditions provided.
Step 1: Calculate the Initial Kinetic Energy
The mass is given an initial velocity of v=−1.0m/s. The kinetic energy KE at this point can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×3kg×(−1.0m/s)2=12×3×1=1.5J
Step 2: Relate Kinetic Energy to Potential Energy
At the maximum compression (which is the amplitude A), all the kinetic energy will be converted into potential energy PE stored in the spring. The potential energy in a spring is given by:
PE=12kA2
Setting the kinetic energy equal to the potential energy at maximum compression:
1.5J=12×1200N/m×A2
Step 3: Solve for Amplitude A
Rearranging the equation to solve for A2:
1.5=600A2⟹A2=1.5600=1400
Taking the square root:
A=√1400=120m=0.05m=5cm
Step 4: Calculate Angular Frequency ω
The angular frequency ω is calculated using the formula:
ω=√km
Substituting the values:
ω=√1200N/m3kg=√400=20rad/s
Step 5: Write the Equation of Motion
The equation of motion for simple harmonic motion (SHM) can be expressed as:
x(t)=Asin(ωt)
Substituting the values of A and ω:
x(t)=120sin(20t)
Final Answers
1. The amplitude of motion is A=5cm.
2. The position as a function of time is:
x(t)=120sin(20t)
The mass is given an initial velocity of v=−1.0m/s. The kinetic energy KE at this point can be calculated using the formula:
KE=12mv2
Substituting the values:
KE=12×3kg×(−1.0m/s)2=12×3×1=1.5J
At the maximum compression (which is the amplitude A), all the kinetic energy will be converted into potential energy PE stored in the spring. The potential energy in a spring is given by:
PE=12kA2
Setting the kinetic energy equal to the potential energy at maximum compression:
1.5J=12×1200N/m×A2
Rearranging the equation to solve for A2:
1.5=600A2⟹A2=1.5600=1400
Taking the square root:
A=√1400=120m=0.05m=5cm
The angular frequency ω is calculated using the formula:
ω=√km
Substituting the values:
ω=√1200N/m3kg=√400=20rad/s
The equation of motion for simple harmonic motion (SHM) can be expressed as:
x(t)=Asin(ωt)
Substituting the values of A and ω:
x(t)=120sin(20t)
1. The amplitude of motion is A=5cm.
2. The position as a function of time is:
x(t)=120sin(20t)
Topper's Solved these Questions
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (PERIOD OF OSCILLATION OF (i) A LIQUID IN A U-TUBE, (ii) TEST TUBE FLOAT, (iii) (iii) A PISTON IN AN ENGINE etc.)
Explore 9 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (FROM ENERGY OF AS.H. OSCILLATOR )
Explore 9 Videos
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
Explore 19 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
Explore 12 Videos
Similar Questions
A body of mass 10 kg initially at rest acquires velocity 10ms−1. What is the work done ?
View SolutionA stone of mass 1 kg is thrown with a velocity of 20ms−1 across the frozen surface of a lake and it comes to rest after travelling a distance of 50m. What is the magnitude of the force opposing the motion of the stone?
View SolutionIn the figure, the position time graph of a particle of mass 0.1 kg is shown. The impulse at t=2 second is :
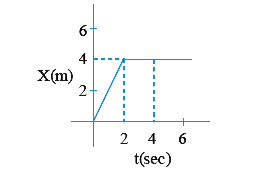
View SolutionA body of mass 6 kg is acted on a by a force so that its velocity changes from 3ms−1 to 5ms−1, then change in momentum is
View SolutionA body of mass 1kg suspended an ideal spring oscillates up and down. The amplitude of oscillation is 1 metre and the periodic time is 1.57 second. Determine.
View SolutionA mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
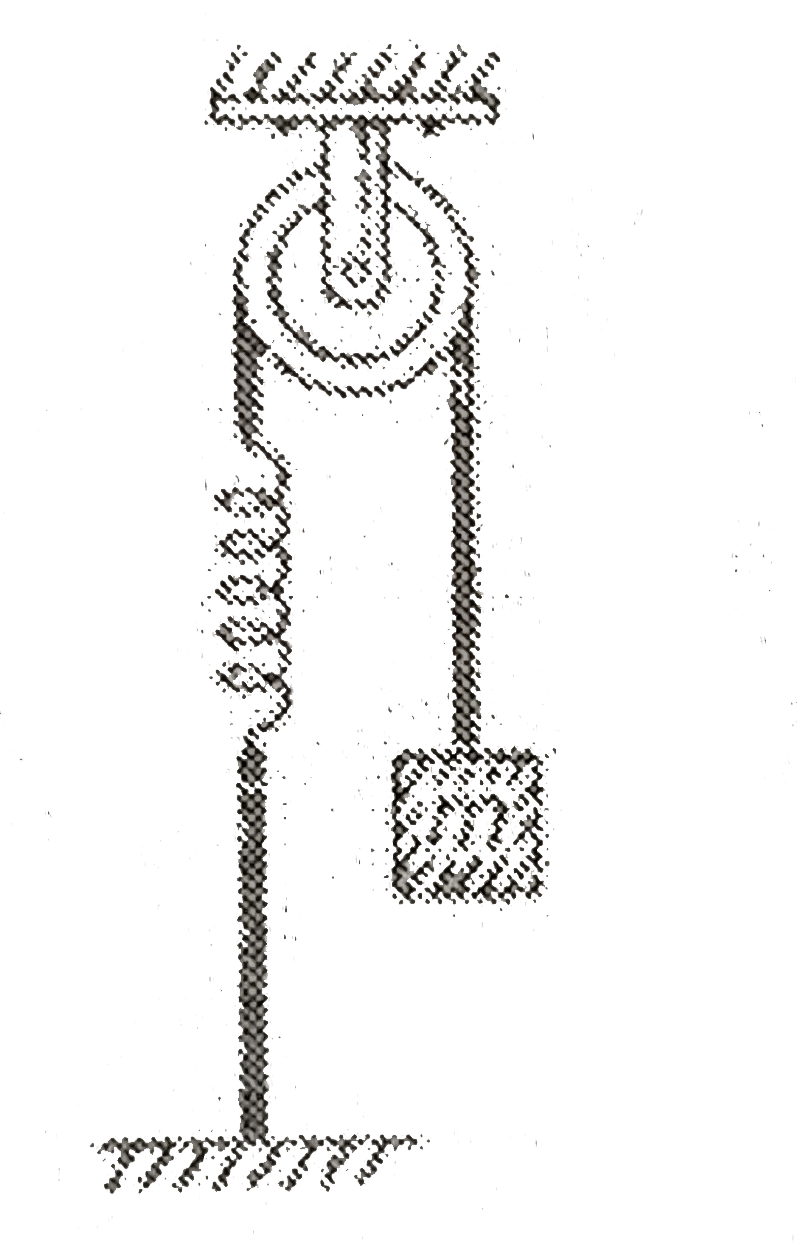
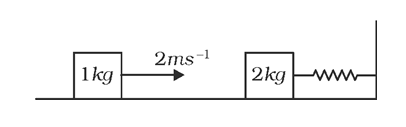
View SolutionA spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0Nm−1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0ms−1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.

View SolutionA particle of mass 0.1kg executes SHM under a force F=−10x(N). Speed of particle at mean position is 6m/s. Find its amplitude of oscillation.
View SolutionA force of 6.4 N stretches a vertical spring by 0.1 m. The mass (in kg) that must be suspended from the spring so that it oscillates with a time period of π4 second.
View Solution