ABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
The correct Answer is:75∘
To find the angle ∠BOC where O is the intersection of lines CE and BD in the given configuration, we can follow these steps:
Step 1: Understand the Configuration
- We have a square ABCD with vertices A,B,C,D.
- Inside this square, there is an equilateral triangle BEC where B and C are two vertices of the square and E is a point inside the square.
Step 2: Identify Angles in the Equilateral Triangle
- In an equilateral triangle, all angles are equal to 60∘.
- Therefore, ∠BEC=60∘.
Step 3: Determine Angles in the Square
- Since ABCD is a square, all angles are 90∘.
- Thus, ∠ABC=90∘ and ∠BCD=90∘.
Step 4: Analyze the Intersection of Lines
- The lines BD and CE intersect at point O.
- We need to find ∠BOC.
Step 5: Use the Angle Properties
- We know that ∠BEC=60∘ (from the equilateral triangle).
- The angle ∠BOC can be found using the property of angles around point O:
∠BOC+∠BEC=180∘
This is because ∠BEC and ∠BOC are supplementary angles.
Step 6: Solve for ∠BOC
- Substitute ∠BEC into the equation:
∠BOC+60∘=180∘
- Rearranging gives:
∠BOC=180∘−60∘=120∘
Final Answer
Thus, the measure of ∠BOC is 120∘.
---
- We have a square ABCD with vertices A,B,C,D.
- Inside this square, there is an equilateral triangle BEC where B and C are two vertices of the square and E is a point inside the square.
- In an equilateral triangle, all angles are equal to 60∘.
- Therefore, ∠BEC=60∘.
- Since ABCD is a square, all angles are 90∘.
- Thus, ∠ABC=90∘ and ∠BCD=90∘.
- The lines BD and CE intersect at point O.
- We need to find ∠BOC.
- We know that ∠BEC=60∘ (from the equilateral triangle).
- The angle ∠BOC can be found using the property of angles around point O:
∠BOC+∠BEC=180∘
This is because ∠BEC and ∠BOC are supplementary angles.
- Substitute ∠BEC into the equation:
∠BOC+60∘=180∘
- Rearranging gives:
∠BOC=180∘−60∘=120∘
Thus, the measure of ∠BOC is 120∘.
Topper's Solved these Questions
- QUADRILATERALBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:QUADRILATERALExercise:EXERCISE
Explore 48 Videos
- PROFIT & LOSSBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:PROFIT & LOSSExercise:Questions
Explore 200 Videos
- RATIO & PROPORTIONBook:ADVANCED MATHS BY ABHINAY MATHS ENGLISHChapter:RATIO & PROPORTIONExercise:QUESTIONS
Explore 113 Videos
Similar Questions
Knowledge Check
ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
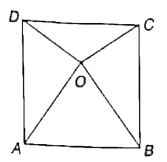 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determinedABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC ?
A15B30C25D10
ABCD is square . BCE is equilateral Δ outside . Find ∠DEC
View SolutionABCD is a square and BCE is an equilateral triangle. Find the value of a,b and reflex ∠BED.
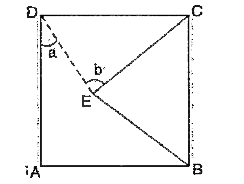
View SolutionABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
View SolutionABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
View SolutionThe equilateral triangle ABP lies inside the square ABCD. Find ∠CPD.
View Solution
