The equilateral triangle ABP lies inside the square ABCD. Find ∠CPD.
150°
145°
155°
160°
The correct Answer is:A
To find the angle ∠CPD in the given configuration, we can follow these steps:
1. Understand the Configuration: We have a square ABCD and an equilateral triangle ABP inside it. The vertices of the square are A,B,C,D in clockwise order.
2. Identify Angles in the Equilateral Triangle: Since ABP is an equilateral triangle, all its angles are 60∘. Therefore, ∠APB=60∘.
3. Determine Angles in the Square: The angles in square ABCD are all 90∘. Specifically, ∠ABC=90∘.
4. Calculate ∠BPC: Since ∠APB=60∘ and ∠ABC=90∘, we can find ∠BPC using the angle sum property:
∠BPC+∠APB+∠ABC=180∘
∠BPC+60∘+90∘=180∘
∠BPC=180∘−150∘=30∘
5. Use Isosceles Triangle Properties: Since PB=AB (sides of the equilateral triangle), we have PB=BC. Thus, △BPC is isosceles with PB=BC. Therefore, ∠BPC=∠BCP=30∘.
6. Calculate Remaining Angles: Now, in triangle BPC:
∠BPC+∠BCP+∠CPB=180∘
30∘+30∘+∠CPB=180∘
∠CPB=180∘−60∘=120∘
7. Determine ∠APD: Since APD is also an isosceles triangle (with AP=AD), we have:
∠APD=∠ADP=75∘
8. Find ∠CPD: The sum of angles around point P is 360∘:
∠CPD+∠APD+∠BPC+∠APB=360∘
∠CPD+75∘+30∘+60∘=360∘
∠CPD+165∘=360∘
∠CPD=360∘−165∘=195∘
Final Answer:
∠CPD=195∘
∠BPC+∠APB+∠ABC=180∘
∠BPC+60∘+90∘=180∘
∠BPC=180∘−150∘=30∘
∠BPC+∠BCP+∠CPB=180∘
30∘+30∘+∠CPB=180∘
∠CPB=180∘−60∘=120∘
∠APD=∠ADP=75∘
∠CPD+∠APD+∠BPC+∠APB=360∘
∠CPD+75∘+30∘+60∘=360∘
∠CPD+165∘=360∘
∠CPD=360∘−165∘=195∘
∠CPD=195∘
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALSBook:S CHAND IIT JEE FOUNDATIONChapter:POLYGONS AND QUADRILATERALSExercise:Question Bank
Explore 29 Videos
- PERIMETER AND AREA Book:S CHAND IIT JEE FOUNDATIONChapter:PERIMETER AND AREA Exercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- POWERS AND ROOTS Book:S CHAND IIT JEE FOUNDATIONChapter:POWERS AND ROOTS Exercise:UNIT TEST-1
Explore 20 Videos
Similar Questions
Knowledge Check
In the figure given below, equilateral triangle ECB surmonunts sqaure ABCD. Find the angle BED represented by x.
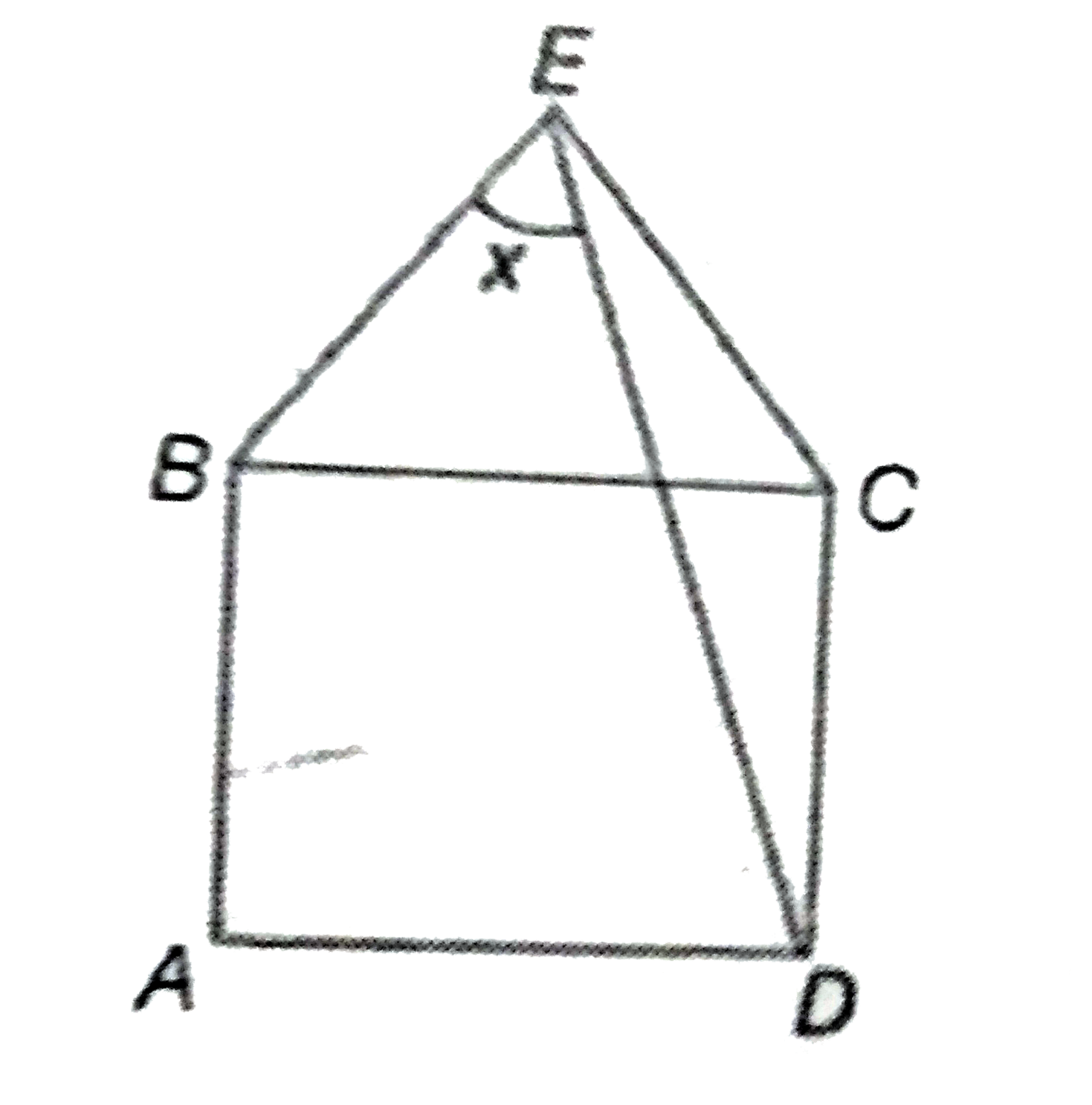 A15∘B30∘C45∘D60∘
A15∘B30∘C45∘D60∘In the given diagram, equilateral triangle EDC surmounts square ABCD. Find the ∠BED represented by x. Where ∠EBC=α∘:
 A45∘B60∘C30∘Dnone of these
A45∘B60∘C30∘Dnone of theseIn the figure ΔABE is an equilateral triangle in a square ABCD. Find the value of angle x in degrees :
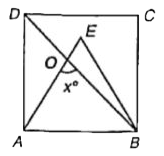 A60∘B45∘C75∘D90∘
A60∘B45∘C75∘D90∘
In the given figure equilateral triangle EDC surmounts the square ABCD. α=
View SolutionABCD is a square. BEC is an equilateral triangle inside the square. If CE & BD intersects at O. Find ∠BOC=?
View SolutionPoint E and F are located on square ABCD so that ABEFis an equilateral triangle. If the length of side of thesquare ABCD is 1 unit, then which of the following is/are cofrect?
View SolutionAn equilateral △TQR is drawn inside a square □ PQRS. The value of the ∠PTS (in degrees) is
View SolutionIf the incentre of an equilateral triangle lies inside the triangle and its radius Is 3 cm, then the side of the equilateral triangle is
View Solution
