State Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor . Solution in Kannada
Statement : The line integral of magnetic field around any closed path in free space is equal to μ0 times the net current enclosed by that path.
i.e., ∮→B.d→I=μ0I
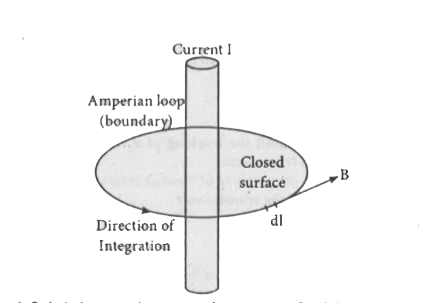
Consider a infinitely long conductor carrying a current . Let Ie be the current enclosed by the loop and L be the length of the loop for which .B. is tangential , then the amperes circuital law ∮→B.d→I=μ0I becomes BL=μ0I
If we assume a straight conductor and the boundary of the surface surrounding the conductor as a circle , then length of the boundary is the circumference , 2πr , where .r. is the radius of the circle . Then B. 2πr=μ0I
∴B=μ0I2πr
Topper's Solved these Questions
- SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY -2015EXERCISE - PART-D
11 Videos
- SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014EXERCISE - PART-D (VI. Answer any three of the following questions.)
5 Videos
- SUPPLEMENTARY EXAM QUESTION PAPER JUNE-2019BOOK - SUNSTAR PUBLICATIONCHAPTER - SUPPLEMENTARY EXAM QUESTION PAPER JUNE-2019EXERCISE - Part-C
18 Videos
Similar Questions
Derive an expression for the electric field at a point due to an infinitely long thin charged straight wire using Gauss Law.
View SolutionTwo charges 3x10−8C & −2x10−8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero? Take the potential infinity to be 0.
View SolutionMention and five properties of electric field lines.
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
View SolutionObtain an expression for the magnetic field at a point due to an infinitely long thin conductor or wire by applying Ampere's circuital law.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionUsing Ampere.s circuital law derive an expression for magnetic field due to infinitely long current carrying wire at a point at distance Yfrom it.
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionState Biot-Savart.s law. Derive an expression for magnetic field at a point near an infinitely long and straight current carrying conductor.
View SolutionState Ampere's circuital law. Derive an expression for magnetic field due to long solenoid .
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionUsing Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View Solution
