Question

Obtain an expression for the total energy of an electron in the $n^{th}$ orbit of hydrogen atom in terms of absolute constants.

Explanation

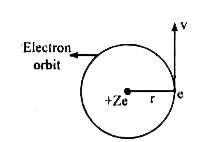
Consider an electron of mass m and charge-e revolving round the nucleus of an atom of atomic number Z in the stationary orbit of radius .r.. Let v be the velocity of the electron. The electron posses potential energy because it is in the electrostatic field of the nucleus it also possess kinetic energy by virtue of its motion.
For stationary orbit, total energy E = KE + PE ...(1)
From Rutherford.s atom model,
For stationary orbit, Centripetal force = Electrostatci force.
`(mv^(2))/( r )=(1)/(4pi epsilon_(0))(Ze)/(r^(2))(-e)`
(`because` Electrostatic force, according to Coulomb.s law)
On dividing by 2 on both sides, we get
`(mv^(2))/(2)=(Ze^(2))/(8pi epsilon_(0)r)`
`KE=(Ze^(2))/(8pi epsilon_(0)r)- - - - (2) " " [because KE=(1)/(2)mv^(2)]`
We have PE = Electric potential at a distance are due to `+Ze xx(-e)`
`PE=(1)/(4pi epsilon_(0))(Ze)/( r )(-e)" "[because V=(1)/(4pi epsilon_(0))(q)/( r )," Hence "q=+Ze]`
`PE=-(Ze^(2))/(4pi epsilon_(0)r)_ _ _ _ to(3)`
Equation (2) and (3) in (1), we get
`E=(Ze^(2))/(4pi epsilon_(0)r)[(1)/(2)-1]`
`E=-(Ze^(2))/(8pi epsilon_(0)r)`