माना f:(−1,1)→R एक ऐसा अवकलनीय फलन है जिसमे f(0)=−1तथा f'(0)=1है। माना g(x)=[f(2f(x)+2)]2 तो g'(0) बराबर है -
−4
0
−2
4
The correct Answer is:A
Step by step video, text & image solution for माना f:(-1,1) to R एक ऐसा अवकलनीय फलन है जिसमे f (0) = -1 तथा f '(0) = 1है। माना g (x)= [f (2f (x) + 2)]^(2) तो g '( 0 ) बराबर है - by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
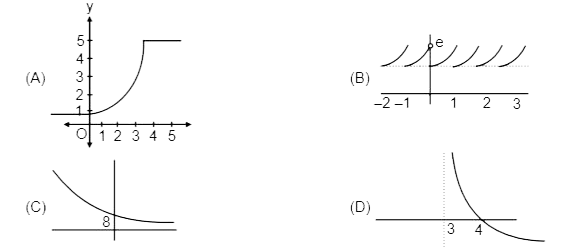
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-04:27View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
04:01View SolutionLet f : (-1,1) to R be a differentiabale function with f(0) = -1 and f'(0) = 1. Let g(x) = [f(2f(x)+2)]^(2) , then g'(0)=
04:01View SolutionLet f : (-1,1) to IR be a differentiable function with f(0) =- 1 and f'(0) =1 IF g(x) ={f(2f(x)+2)}^2 , then g'(0) =
06:04View SolutionLet f:(−1,1)→IR be a differentiable function with f(0) =- 1 and f'(0) =1 IF g(x)={f(2f(x)+2)}2, then g'(0) =
03:35View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
01:45View Solutionयदि ∫(x+1)√2x−1dx=f(x)√2x−1+C है, जहाँ C एक समाकलन अचर है, तो f(x) बराबर है
01:41View Solutionमाना कि f:R→R फलन f(x)=√x−3,∀x∈R द्वारा परिभाषित है, तब f−1(x)⇒
02:07View SolutionLet f:(-1,1)toR be a differentiable function with f(0)=-1 and f'(0)=1 . Let g(x)=[f(2f(x)+2)]^(2) . Then g'(0)=
01:25View Solutionमाना f(x+y)+f(x-y)=2f (x)f(y) , AA x , y in R And f(0) ne 0 , Then the value of f (2) is if f (1) = k
03:49View Solutionमाना f(x+y)+f(x-y)=2f (x)f(y) , AA x , y in R And f(0) ne 0 , Then if f (1) = k then f (3) - 2kf (2) is the value of
01:27View Solutionयदि ∫.(−1,1)→R अवकलनीय फलन है तथा f(0)=−1 तथा f(0)=1 माना g(x)=[f{2f(x)+2}]2,तबg'(0) है
02:35View Solutionagreed f={(1,1),(2,4),(0,-2),(-1,-5)},Z से Z में एक रैखिक फलन तब f(x) है
04:55View Solutionमाना f:(−1,1)→R एक ऐसा अवकलनीय फलन है जिसमे f(0)=−1 तथा f'(0)=1 है | माना g(x) =[f(2f(x)+2)]2 तो g'(0) बराबर है :
View SolutionLet f : (-1,1) to R be a differentiable function with f(0) = -1 and f'(0) = 1 . Let g(x) = [f(2f(x)+2)]^(2) , then g'(0)=
View Solution
