यदि y=Ae−ktcos(pt+c), तो दर्शाइए कि d2ydt2+2kdydt+n2y=0, जहां n2=p2+k2
The correct Answer is:B
Step by step video, text & image solution for यदि y = Ae^(-kt) cos (pt+c), तो दर्शाइए कि (d^(2)y)/(dt^(2))+2k (dy)/(dt)+n^(2)y=0, जहां n^(2) =p^(2) + k^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
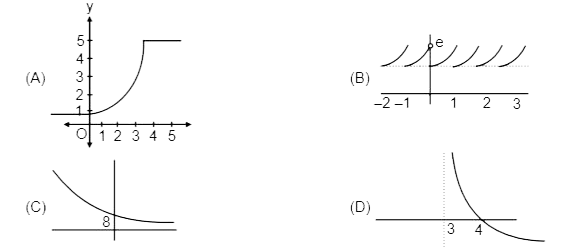
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
View SolutionIf y = e^(kt) then (dy)/(dt) will be (A) e^(kt) (B) (e^(kt))/(k) (C) te^(kt) (D ) to^(kt)
View SolutionIf y=Ae−ktcos(pt+c), then prove that d2ydt2+2kdydx+n2y=0 , where n2=p2+k2
View SolutionThe second derivative of a single valued function parametrically represented by x=φ(t)andy=ψ(t) (where φ(t)andψ(t) are different function and φ′(t)≠0 ) is given by d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)2 d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt)(dydt2)−(dxdt□)d2ydt2(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt2)(dydt□)−(d2xdt2)dydt□(dxdt)3
View Solutionif y=Ae^(mx)+Be^(nx) then prove that (d^(2)y)/(dx^(2))-(m+n)(dy)/(dx)+mny=0
View Solutionयदि (If) y=Aektcos(pt+α), दिखाएँ कि (show that) d2ydx2−2kdydt+(p2+k2)y=0
View SolutionIf y=Aemx+Benx, prove that d2ydx2−(m+n)dydx+mny=0.
View Solutionयदि y=(x+√x2+1)m, तो सिध्द कीजिए कि (x2+1)d2ydx2+xdydx−m2y=0
View Solutionयदि y=Ae−ktcos(pt+c), तो दर्शाइए कि d2ydt2+2kdydt+n2y=?, जहां n2=p2+k2
View SolutionIf x=Ae−kt2cos(pt+∈), and A,k,p,∈ are constants, show that d2xdt2+kdxdt+n2x=0, where n2=p2+14k2.
View Solutionयदि x=tan(1alogy) है तो दर्शाइए कि
(1+x2)d2ydx2+(2x−a)dydx=0
View Solutionx=Ae−kt2cos(pt+ε)হলে এবং A,k,p,ε ধ্রুবক হলে, দেখাও যে, d2xdt2+kdxdt+n2x=0,যেখানে n2=p2+(14)k2
View SolutionThe equation d2ydt2+bdydt+ω2y=0 represents the equation of motion for a……………….vibration.
View SolutionThe second derivative of a single valued function parametrically represented by x=φ(t)andy=ψ(t) (where φ(t)andψ(t) are different function and φ′(t)≠0 ) is given by d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)2 d2ydx2=⎛⎜ ⎜⎝(dxdt)(d2ydt2)−(d2xdt2)dydt(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt)(dydt2)−(dxdt□)d2ydt2(dxdt)3 d2ydx2=⎛⎜ ⎜⎝(d2xdt2)(dydt□)−(d2xdt2)dydt□(dxdt)3
View Solution
