माना कि x2x−2xxcoty−1=0 द्वारा परिभाषित x का एक अस्पष्ट फलन है । तब y'(1) बराबर है :
1
log2
−log2
−1
The correct Answer is:D
Step by step video, text & image solution for माना कि x^(2x) - 2x^(x) cot y - 1 = 0 द्वारा परिभाषित x का एक अस्पष्ट फलन है । तब y'(1) बराबर है : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
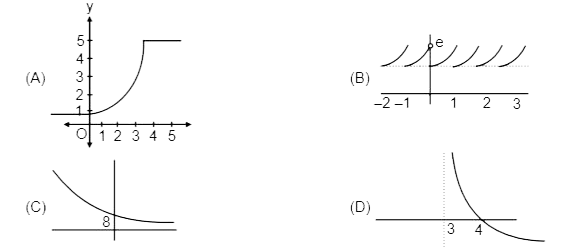
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-
View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solution{(x,y):y2≤2x तथा y≥4x−1} द्वारा परभाषित क्षेत्र का क्षेत्रफल है :
View Solutionमाना y=y(x), अवकल समीकरण (x2+1)2dydx+2x(x2+1)y=1 का हल है, जबकि y(0) = 0 है। यदि √ay(1)=π32 है तो 'α' का मान है
View Solutionयदि अवकल समीकरण dydx+(2x+1x)y=e−2x,x>0 का हल y(x) है , जहाँ y(1)=12e−2, तो
View Solutionयदि ∫(x+1)√2x−1dx=f(x)√2x−1+C है, जहाँ C एक समाकलन अचर है, तो f(x) बराबर है
View Solutionlimx→0xcot(4x)sin2xcot2(2x) बराबर है
View Solutionमाना y = y(x) अवकल समीकरण xdydx+y=xlogex,(x>1) का हल है । यदि 2y(2)=loge4−1 है, तो y(e) बराबर है
View Solutionयदि 3x=4x−1 तब x बराबर है
View Solutionमाना फलन निम रूप से परिभाषित है
f(x)={sin−1λ+x2,0<x<12x,x≥1
x = 1 पर F(x) का मान निम्निष्ठ होगा, यदि λ का मान है
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionमाना कि f:R→R फलन f(x)=√x−3,∀x∈R द्वारा परिभाषित है, तब f−1(x)⇒
View Solutionअंतराल [0, 2] में f(x)=2+(x−1)2/3 द्वारा परिभाषित फलन f है | निम्न में से कौन सही नहीं है ?
View Solutionयदि वास्तविक चर का वास्तविक मान फलन । इस प्रकार है कि 1(1+x)(1+x2)=A1+x+f(x)1+x2 है तो f (x) किसके बराबर है?
View Solutionफलन y=2x1+2x का व्युत्क्रम है
View Solution
