यदि f(x)=∣∣ ∣ ∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin2x2∣∣ ∣ ∣∣ हो तो
f(−2)=0
f'(−1/2)=0
f'(−1)=−2
f''(0)=4
The correct Answer is:B
Step by step video, text & image solution for यदि f (x) = |{:( cos ( x + x ^(2)), sin (x + x ^(2)) , - cos ( x + x ^(2))), ( sin (x -x ^(2)), cos (x-x ^(2)), sin (x - x ^(2))), (sin 2x, 0, sin 2x ^(2)):}| हो तो by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
फलन f1(x)=⎧⎪⎨⎪⎩1यदिx≤0x2+1यदि0<x<25यदिx≥2,f2(x)=log1/2(x−3),f3(x)=23−x तथा f4(x)=e{x} जहाँ {.} भिन्नात्मक भागफलन को प्रदर्शित करता है, के आरेख निम्न (क्रम में नहीं) है-
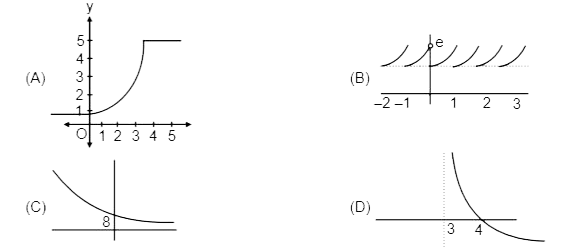
फलन f1(x),f2(x),f3(x) एवं f4(x) के आरेखों का सही क्रम होगा-02:26View Solutionf(x)=cos(sin(ln(x2+ex2+1)))+sin(cos(ln(x2+ex2+1)))
02:13View SolutionLet f(x)=∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin(2x2)∣∣ . Find the value of f′(0).
06:12View SolutionCompute the following: [cos2xsin2xsin2xcos2x]+[sin2xcos2xcos2xsin2x]
03:28View SolutionLet f(x)=∣∣ ∣ ∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin(2x2)∣∣ ∣ ∣∣.
Find the value of f'(0).05:00View Solution(cos^(3) x- sin^(2) x)/(cos x - sin x)=(1)/(2) (2 + sin 2x)
07:41View SolutionThe values of x in (0,π) satisfying the equation.
∣∣ ∣ ∣∣1+sin2xsin2xsin2xcos2x1+cos2xcos2x4sin2x4sin2x1+4sin2x∣∣ ∣ ∣∣=0, are03:28View SolutionProve that sin3x+sin2x−sinx=4sinxcosx2cos3x2
03:40View SolutionProve that: sin3x+sin2x−sinx=4sinxcosx2cos3x2
02:23View SolutionLet f(x)=∣∣ ∣ ∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin(2x2)∣∣ ∣ ∣∣ . Find the value of f′(0).
05:00View SolutionLet f(x)=∣∣ ∣ ∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin(2x2)∣∣ ∣ ∣∣.
Find the value of f'(0).04:43View SolutionLet f(x)=∣∣ ∣ ∣∣cos(x+x2)sin(x+x2)−cos(x+x2)sin(x−x2)cos(x−x2)sin(x−x2)sin2x0sin(2x2)∣∣ ∣ ∣∣.
Find the value of f'(0).05:14View Solutionf(x)=∣∣ ∣ ∣∣sin2x1+cos2xcos2x1+sin2xcos2xcos2xsin2xcos2xsin2x∣∣ ∣ ∣∣,x∈R का अधिकतम मान है।
02:16View SolutionThe values of x in (0,π) satisfying the equation.
∣∣ ∣ ∣∣1+sin2xsin2xsin2xcos2x1+cos2xcos2x4sin2x4sin2x1+4sin2x∣∣ ∣ ∣∣=0, are03:48View SolutionCompute the following: [cos2xsin2xsin2xcos2x]+[sin2xcos2xcos2xsin2x]
08:02View Solution


