In an L-C-R series circuit, the potential difference between the terminals of the inductance is 60 V, between the terminals of the capacitor is 30 V and that across the resistance is 40 V. Then, the supply voltage will be equal to
10 V
50 V
70 V
130 V
The correct Answer is:B
To find the supply voltage Vs in an L-C-R series circuit, we can use the relationship between the voltages across the inductor VL, capacitor VC, and resistor VR.
Step 1: Identify the given values
- Voltage across the inductor VL=60V
- Voltage across the capacitor VC=30V
- Voltage across the resistor VR=40V
Step 2: Understand the phasor relationship
In an L-C-R series circuit, the voltages across the inductor and capacitor are out of phase by 180 degrees. This means we can treat them as vector quantities where:
- VL and VC will subtract from each other.
- VR is in phase with the supply voltage Vs.
Step 3: Calculate the net voltage across the inductor and capacitor
The net voltage across the inductor and capacitor can be calculated as:
VLC=VL−VC=60V−30V=30V
Step 4: Apply the Pythagorean theorem
The supply voltage Vs can be calculated using the Pythagorean theorem, since VR is in phase with Vs:
Vs=√V2LC+V2R
Substituting the values we have:
Vs=√(30V)2+(40V)2
Step 5: Calculate the squares
Calculating the squares:
Vs=√900+1600
Step 6: Sum the squares
Vs=√2500
Step 7: Take the square root
Vs=50V
Final Answer
The supply voltage Vs is 50V.
---
- Voltage across the inductor VL=60V
- Voltage across the capacitor VC=30V
- Voltage across the resistor VR=40V
In an L-C-R series circuit, the voltages across the inductor and capacitor are out of phase by 180 degrees. This means we can treat them as vector quantities where:
- VL and VC will subtract from each other.
- VR is in phase with the supply voltage Vs.
The net voltage across the inductor and capacitor can be calculated as:
VLC=VL−VC=60V−30V=30V
The supply voltage Vs can be calculated using the Pythagorean theorem, since VR is in phase with Vs:
Vs=√V2LC+V2R
Substituting the values we have:
Vs=√(30V)2+(40V)2
Calculating the squares:
Vs=√900+1600
Vs=√2500
Vs=50V
The supply voltage Vs is 50V.
Similar Questions
Knowledge Check
In a series LCR circuit, the voltage across the resistance, capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
A10VB10√2VC10√2VD20V
In the L-R circuit as shown in figure, potential difference across the resistance at some instant is 4 V. Then
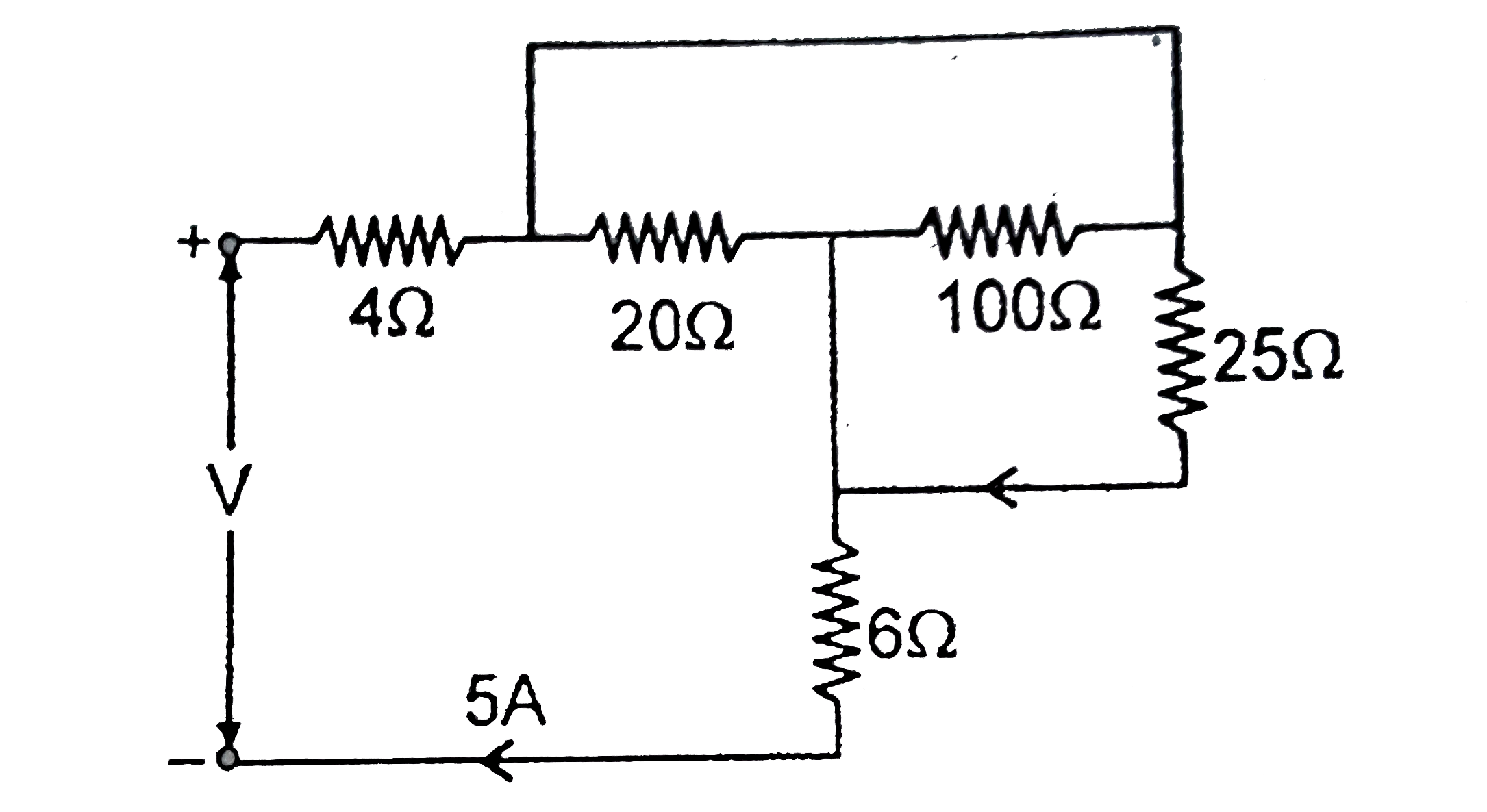
View SolutionIn the circuit shown, the potential difference between A and B VAandVB is equal to_______V.
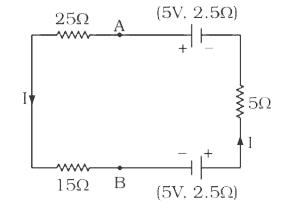
View SolutionIn R-L-C series circuit, the potential difference across each element is 20 V. Now the value of hte resistance alone is doubled, then PD across R, L and C respectively.
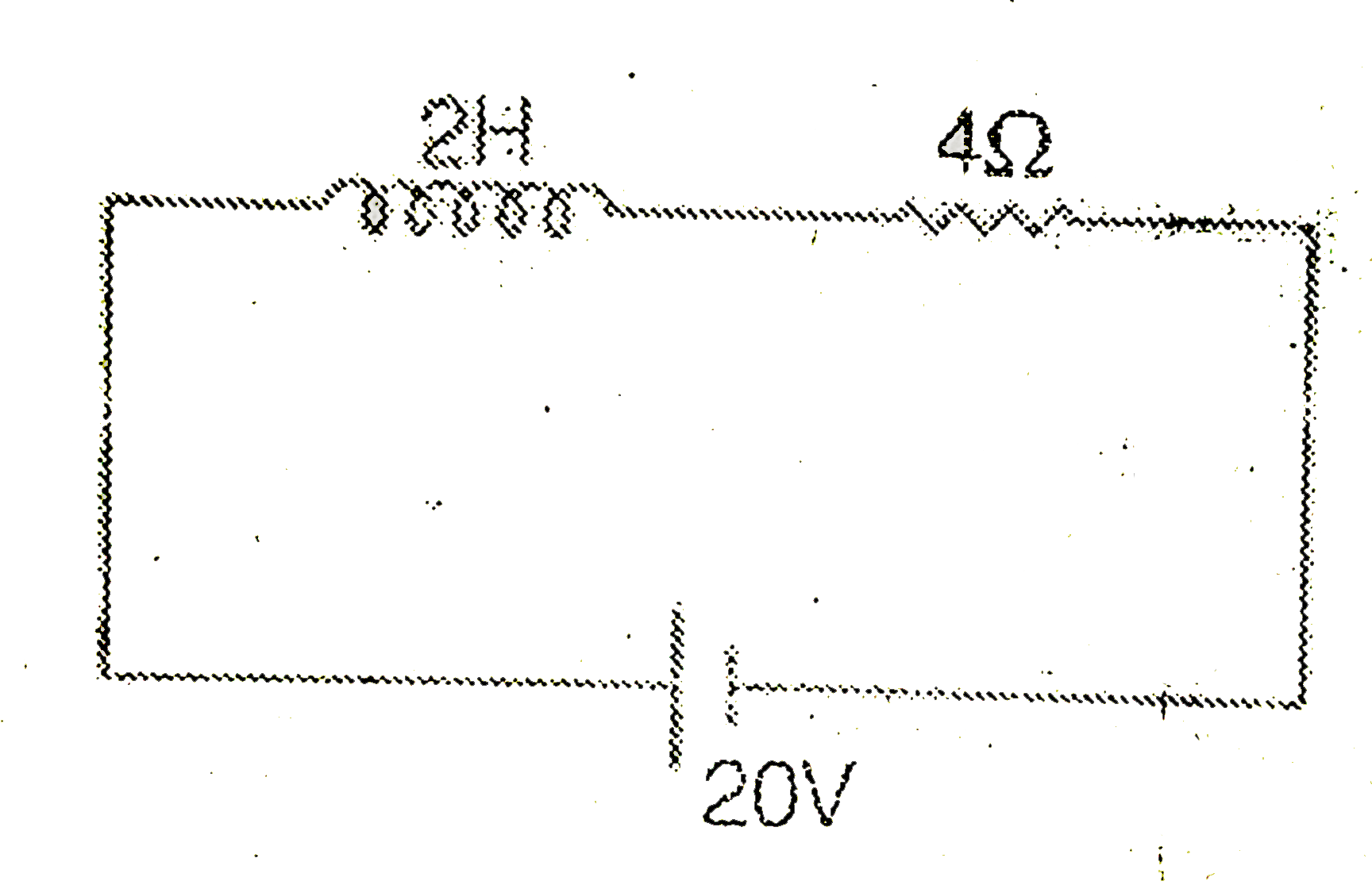
View SolutionIn the circuit shown, the potential difference between the points G and H, VG−VH is equal to _________ V.
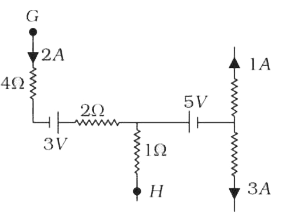
View SolutionIn a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionA voltmeter reads the potential difference across the terminals of an old battery as 1.40V, while a potentiometer reads its voltage to be 1.55V. The voltmeter resistance is 280Ω.
View Solution