In R-L-C series circuit, the potential difference across each element is 20 V. Now the value of hte resistance alone is doubled, then PD across R, L and C respectively.
20 V, 10 V , 10V
20 V, 20 V, 20V
20 V, 40 V, 40 V
10 V, 20 V, 20 V
The correct Answer is:A
To solve the problem step by step, we will analyze the behavior of the R-L-C series circuit when the resistance is doubled.
Step 1: Understand the Initial Conditions
In the given R-L-C series circuit, the potential difference (PD) across each element (R, L, and C) is initially 20 V. This indicates that the circuit is in resonance, where:
- VR=VL=VC=20V
Step 2: Analyze the Effect of Doubling the Resistance
When the resistance R is doubled, the new resistance becomes R′=2R.
Step 3: Determine the Current in the Circuit
In a series circuit, the current I is given by:
I=VZ
Where Z is the impedance of the circuit. At resonance:
Z=R
Thus, the initial current I can be expressed as:
I=VR
Given that V=20V, we have:
I=20R
Step 4: Calculate the New Current After Doubling Resistance
After doubling the resistance, the new current I′ becomes:
I′=VR′=V2R=202R=10R
This shows that the new current is half of the original current:
I′=I2
Step 5: Calculate the New Potential Differences
Using Ohm's Law, the potential difference across each component can be calculated:
1. For the resistor (R):
V′R=I′⋅R′=10R⋅2R=20V
2. For the inductor (L):
Since the circuit is still in resonance, the potential difference across the inductor will equal the potential difference across the capacitor:
V′L=V′C=I′ωL
But since I′=10R and at resonance VL=VC:
V′L=V′C=10V
Conclusion
After doubling the resistance, the potential differences across the components are:
- V′R=20V
- V′L=10V
- V′C=10V
Final Answer
The potential differences across R, L, and C respectively are:
- VR=20V
- VL=10V
- VC=10V
In the given R-L-C series circuit, the potential difference (PD) across each element (R, L, and C) is initially 20 V. This indicates that the circuit is in resonance, where:
- VR=VL=VC=20V
When the resistance R is doubled, the new resistance becomes R′=2R.
In a series circuit, the current I is given by:
I=VZ
Where Z is the impedance of the circuit. At resonance:
Z=R
Thus, the initial current I can be expressed as:
I=VR
Given that V=20V, we have:
I=20R
After doubling the resistance, the new current I′ becomes:
I′=VR′=V2R=202R=10R
This shows that the new current is half of the original current:
I′=I2
Using Ohm's Law, the potential difference across each component can be calculated:
1. For the resistor (R):
V′R=I′⋅R′=10R⋅2R=20V
Since the circuit is still in resonance, the potential difference across the inductor will equal the potential difference across the capacitor:
V′L=V′C=I′ωL
But since I′=10R and at resonance VL=VC:
V′L=V′C=10V
After doubling the resistance, the potential differences across the components are:
- V′R=20V
- V′L=10V
- V′C=10V
The potential differences across R, L, and C respectively are:
- VR=20V
- VL=10V
- VC=10V
Similar Questions
Knowledge Check
- Question 1 - Select One
An LCR series ac circuit is at resonance with 10 V each across L, C and R. If the resistance is halved, the respective voltage across L, C and R are
A10 V, 10 V and 5 VB10 V, 10 V and 10 VC20 V, 20 V and 5 VD20 V, 20 V and 10 V
In the circuit, V is potential differences across the terminal as shwon in figure. Then the value of V is
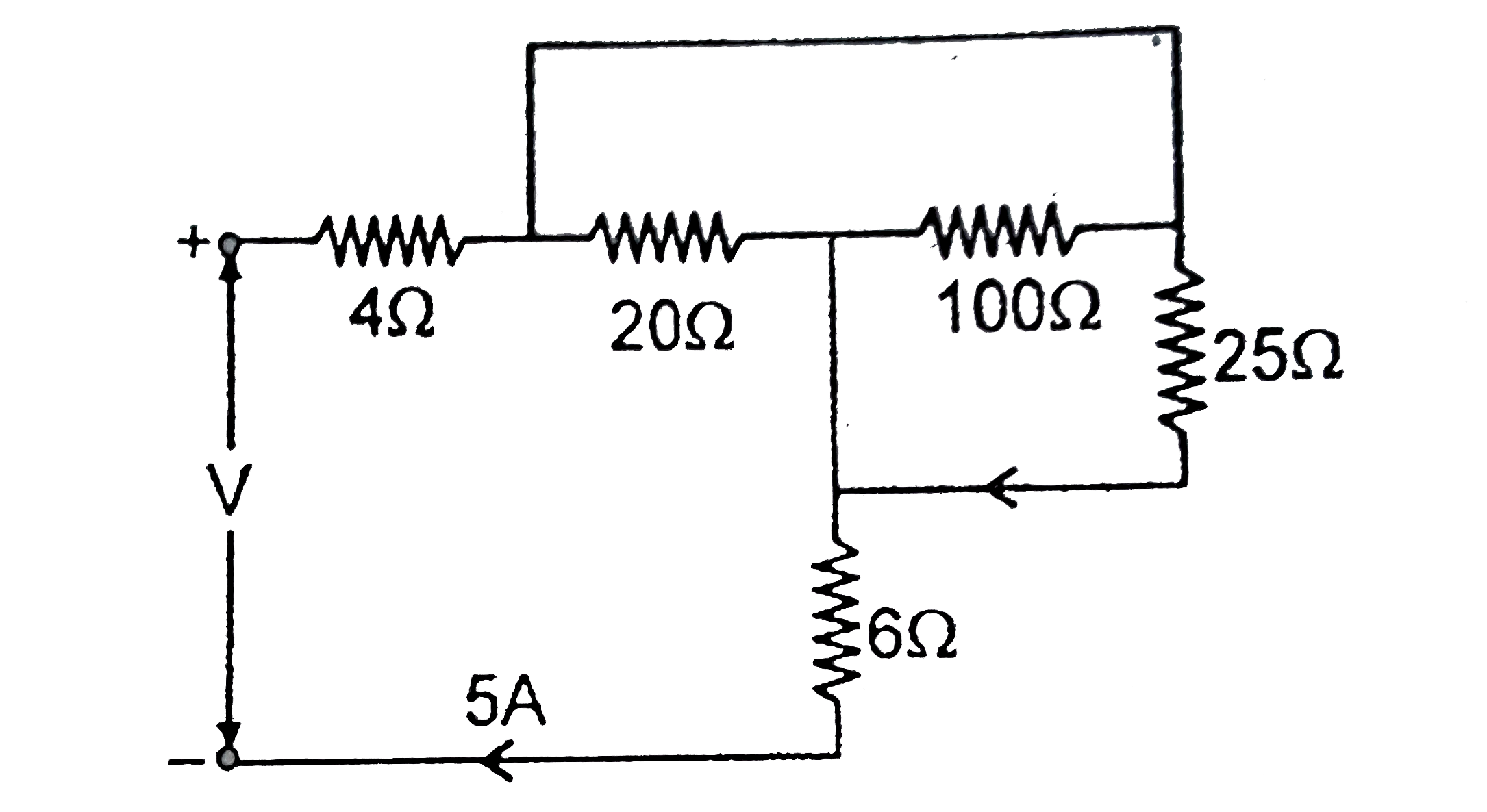 View Solution
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
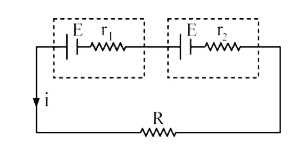 View Solution
View SolutionIn an L-C-R series, AC circuit at resonance
View SolutionIn an L-C-R series circuit, the potential difference between the terminals of the inductance is 60 V, between the terminals of the capacitor is 30 V and that across the resistance is 40 V. Then, the supply voltage will be equal to
View SolutionIn the L-R circuit as shown in figure, potential difference across the resistance at some instant is 4 V. Then
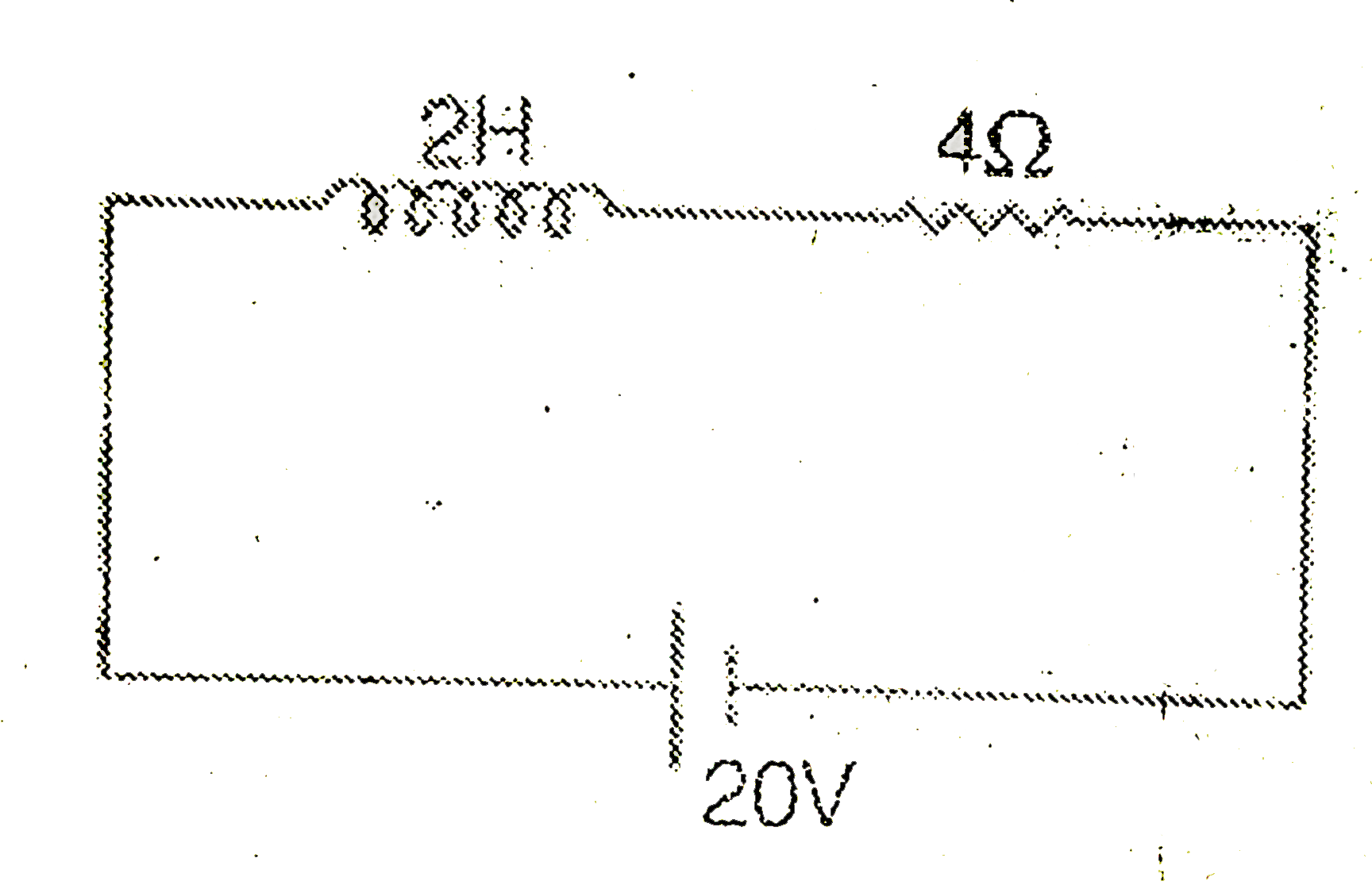 View Solution
View SolutionIn an LCR series ac circuit , the voltage across each of the components , L,C and R is 50 V . The voltage across the LC combination will be :
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View Solution
