A wire of length 1m is moving at a speed of 2ms−1 perpendicular to its length and a homogeneous magnetic field of 0.5T. The ends of the wire are joined to a circuit of resistance 6Ω. The rate at which work is being done to keep the wire moving at constant speed is
1W
13W
16W
112W
The correct Answer is:C
To solve the problem, we need to find the rate at which work is being done to keep the wire moving at a constant speed in a magnetic field. This can be calculated using the concepts of electromagnetic induction and power.
1. Identify the Given Values:
- Length of the wire (L) = 1 m
- Speed of the wire (v) = 2 m/s
- Magnetic field (B) = 0.5 T
- Resistance of the circuit (R) = 6 Ω
2. Calculate the Electromotive Force (EMF):
The induced EMF (E) in the wire moving in a magnetic field can be calculated using the formula:
E=B⋅L⋅v
Substituting the values:
E=0.5T⋅1m⋅2m/s=1V
3. Calculate the Current (I) in the Circuit:
Using Ohm's law, the current (I) can be calculated as:
I=ER
Substituting the values:
I=1V6Ω=16A
4. Calculate the Power (P):
The power (P) can be calculated using the formula:
P=I2⋅R
Substituting the values:
P=(16A)2⋅6Ω=136⋅6=16W
5. Conclusion:
The rate at which work is being done to keep the wire moving at constant speed is:
P=16W
Final Answer:
The rate at which work is being done is 16W.
---
- Length of the wire (L) = 1 m
- Speed of the wire (v) = 2 m/s
- Magnetic field (B) = 0.5 T
- Resistance of the circuit (R) = 6 Ω
The induced EMF (E) in the wire moving in a magnetic field can be calculated using the formula:
E=B⋅L⋅v
Substituting the values:
E=0.5T⋅1m⋅2m/s=1V
Using Ohm's law, the current (I) can be calculated as:
I=ER
Substituting the values:
I=1V6Ω=16A
The power (P) can be calculated using the formula:
P=I2⋅R
Substituting the values:
P=(16A)2⋅6Ω=136⋅6=16W
The rate at which work is being done to keep the wire moving at constant speed is:
P=16W
The rate at which work is being done is 16W.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the emf induced in the wire is 2 V, then the magnitude of the field in tesla is
View SolutionA wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire

View SolutionA horizontal wire 0.8m long is falling at a speed of 5m/s perpendicular to a uniform magnetic field of 1.1T, which is directed from east to west. Calculate the magnitude of the induced ernf. Is the north or south end of the wire positive?
View SolutionA metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionAs shown in figure, a metal rod completes the circuit. The circuit area is perpendicular to a magnetic field with B=0.15T. If the resistance of the total circuit is 3Ω, how large a force is needed to move the rod as indicated with a constant speed of 2 m/s?
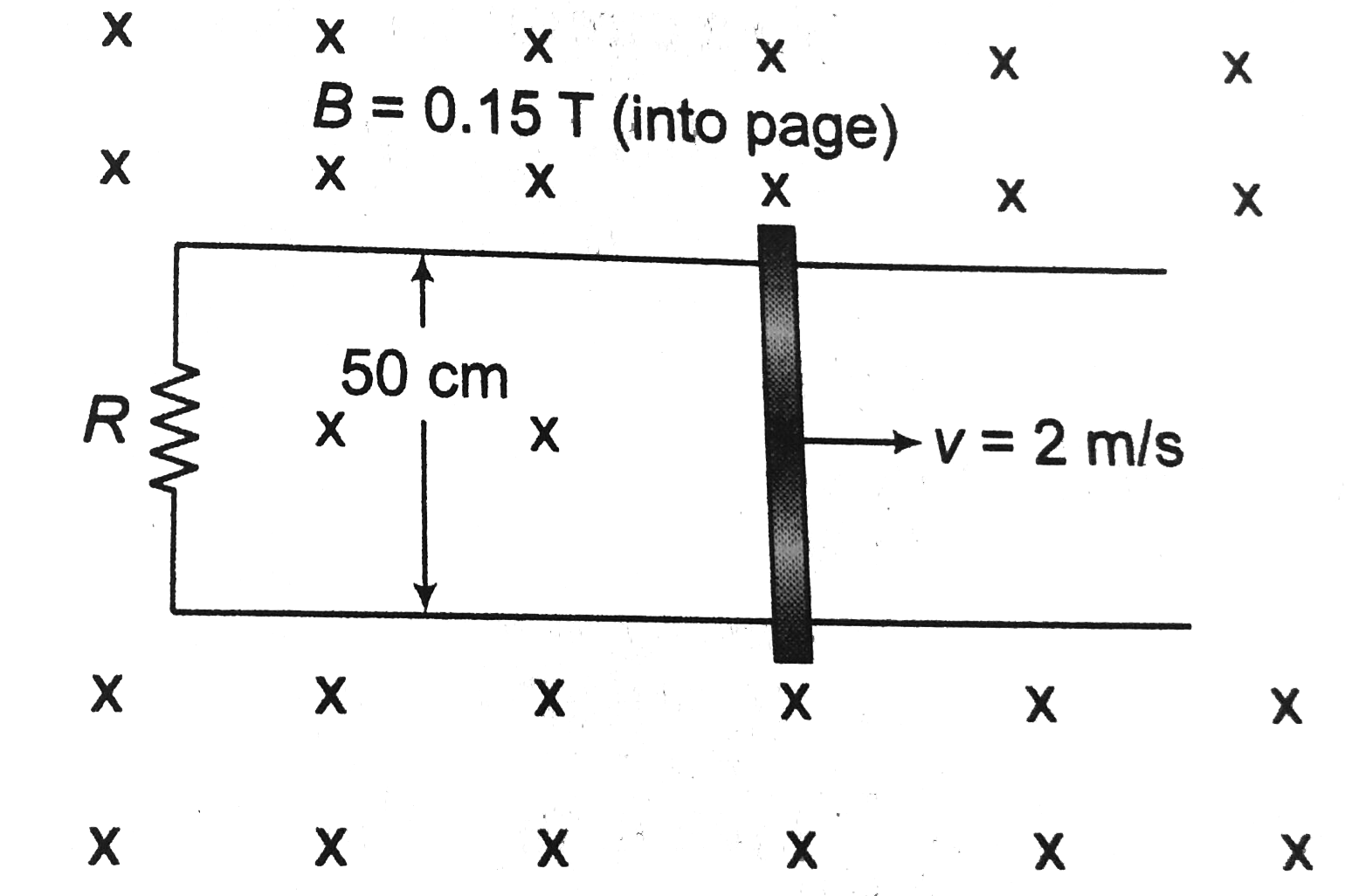
View SolutionA metallic wire PQ of length 1cm moves with a velocity of 2m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2T.Find the emf induced between the ends of the wire.Which end will be positively charged.

View Solution1.2 amp current is flowing in a wire of 0.3 m length, It is placed perpendicular to the magnetic field (identical to 2T). The force acting on the wire will be:
View SolutionA 0.5m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15T. If the resistance of the total circuit is 3Ω calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1
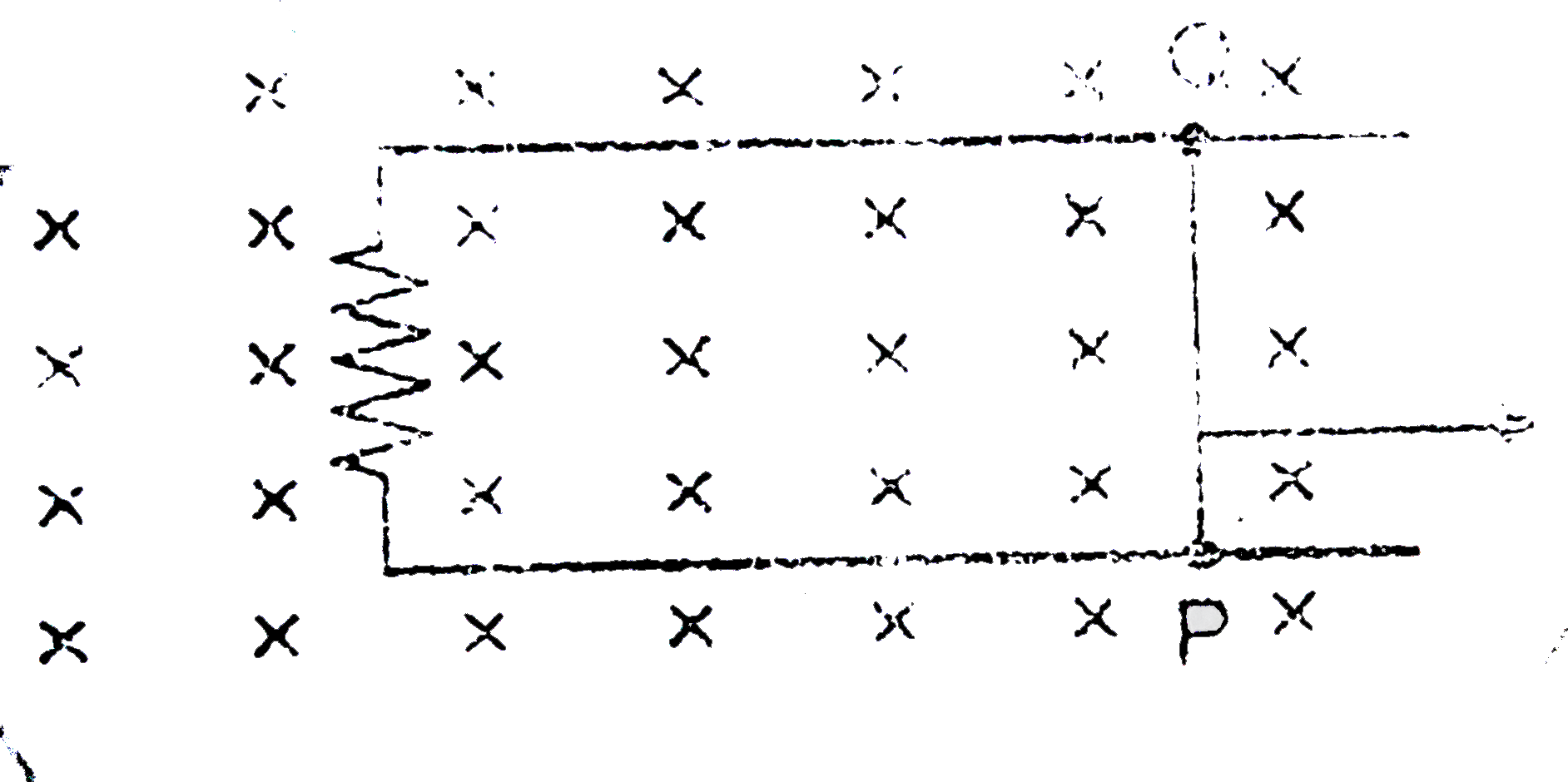
View SolutionA current of 1 A flows a wire of length 0.1 m in a magnetic field of 0.5 T. The force acting on the wire when it makes an angle of 90∘ with the field is
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View Solution
