A straight conductor of length 0.4 m is moved with a speed of 7 m/s perpendicular to the magnetic field of intensity of 0.9Wb/m2. The induced e.m.f. across the conductor will be
5.04 V
1.26 V
2.52 V
25.2 V
The correct Answer is:C
To solve the problem of finding the induced e.m.f. across a straight conductor moving in a magnetic field, we can follow these steps:
1. Identify the Given Values:
- Length of the conductor (L) = 0.4 m
- Speed of the conductor (V) = 7 m/s
- Magnetic field intensity (B) = 0.9 Wb/m²
2. Understand the Formula for Induced e.m.f.:
The induced e.m.f. (E) in a conductor moving through a magnetic field can be calculated using the formula:
E=L×V×B×sin(θ)
where:
- E is the induced e.m.f.
- L is the length of the conductor.
- V is the speed of the conductor.
- B is the magnetic field intensity.
- θ is the angle between the direction of the magnetic field and the direction of motion of the conductor.
3. Determine the Angle:
In this problem, the conductor is moved perpendicular to the magnetic field, which means:
θ=90∘
Therefore, sin(90∘)=1.
4. Substitute the Values into the Formula:
Now, substituting the known values into the formula:
E=0.4m×7m/s×0.9Wb/m2×sin(90∘)
E=0.4×7×0.9×1
5. Calculate the Induced e.m.f.:
Performing the multiplication:
E=0.4×7=2.8
E=2.8×0.9=2.52V
6. Final Answer:
The induced e.m.f. across the conductor is:
E=2.52V
- Length of the conductor (L) = 0.4 m
- Speed of the conductor (V) = 7 m/s
- Magnetic field intensity (B) = 0.9 Wb/m²
The induced e.m.f. (E) in a conductor moving through a magnetic field can be calculated using the formula:
E=L×V×B×sin(θ)
where:
- E is the induced e.m.f.
- L is the length of the conductor.
- V is the speed of the conductor.
- B is the magnetic field intensity.
- θ is the angle between the direction of the magnetic field and the direction of motion of the conductor.
In this problem, the conductor is moved perpendicular to the magnetic field, which means:
θ=90∘
Therefore, sin(90∘)=1.
Now, substituting the known values into the formula:
E=0.4m×7m/s×0.9Wb/m2×sin(90∘)
E=0.4×7×0.9×1
Performing the multiplication:
E=0.4×7=2.8
E=2.8×0.9=2.52V
The induced e.m.f. across the conductor is:
E=2.52V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Aconductor of lengfht 0.4 m is moving with a speed of 7 m/s perpendicular to a magnetic field of intensity0.9Wb/m2 .The induced emf across the coduct is
View SolutionA conductor of length 5 cm is moved paralllel to itself with a speed of 2m/s, perpendicular to a uniform magnetic field of 10−3Wb/m2. the induced emf generated is
View SolutionA conductor of length 5 cm is moved paralllel to itself with a speed of 2m/s, perpendicular to a uniform magnetic field of 10−3Wb/m2. the induced emf generated is
View SolutionA conductor of 3m in length is moving perpendicularly to magnetic field of 10−4 tesla with the speed of 102m/s, then the e.m.f. produced across the ends of conductor will be
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
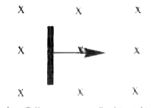
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
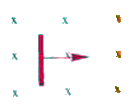
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity ω . The induced e.m.f between the two ends is
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the emf induced in the wire is 2 V, then the magnitude of the field in tesla is
View SolutionA vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is θ. The induced e.m.f. in the rod is
View Solution
