A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
πa2μ0I2bωcosωt
πa2μ0I2bωsinω2t2
πa2μ0I2bωsinωt
πa2μ0I2bωsin2ωt
The correct Answer is:C
We know that, e = NBA ωsinωt
where, N = number of loops = 1
B=μ0I2bN/A−m⇒A=πa2m2
∴ e=μ0I2b(πa2)ωsinωt
⇒ =πa2μ0I2b.ωsinωt
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A very small circular loop of area 5×10−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.1m . A constant current of 1A is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux linked with the smaller loop, (b) induced emf (c) induced current in the smaller loop, as a function of time.
View SolutionAt the centre of a fixed large circular coil of radius R a much smaller circular coil of radius r is placed .The two coils are concentric and are in the same plane .The larger coil carries a current I The smaller coil is set to rotate with a constant angular velocity ω about an axis along their common diameter .Calculate the emf induced in the smaller coil after a time t of its start of ratation
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
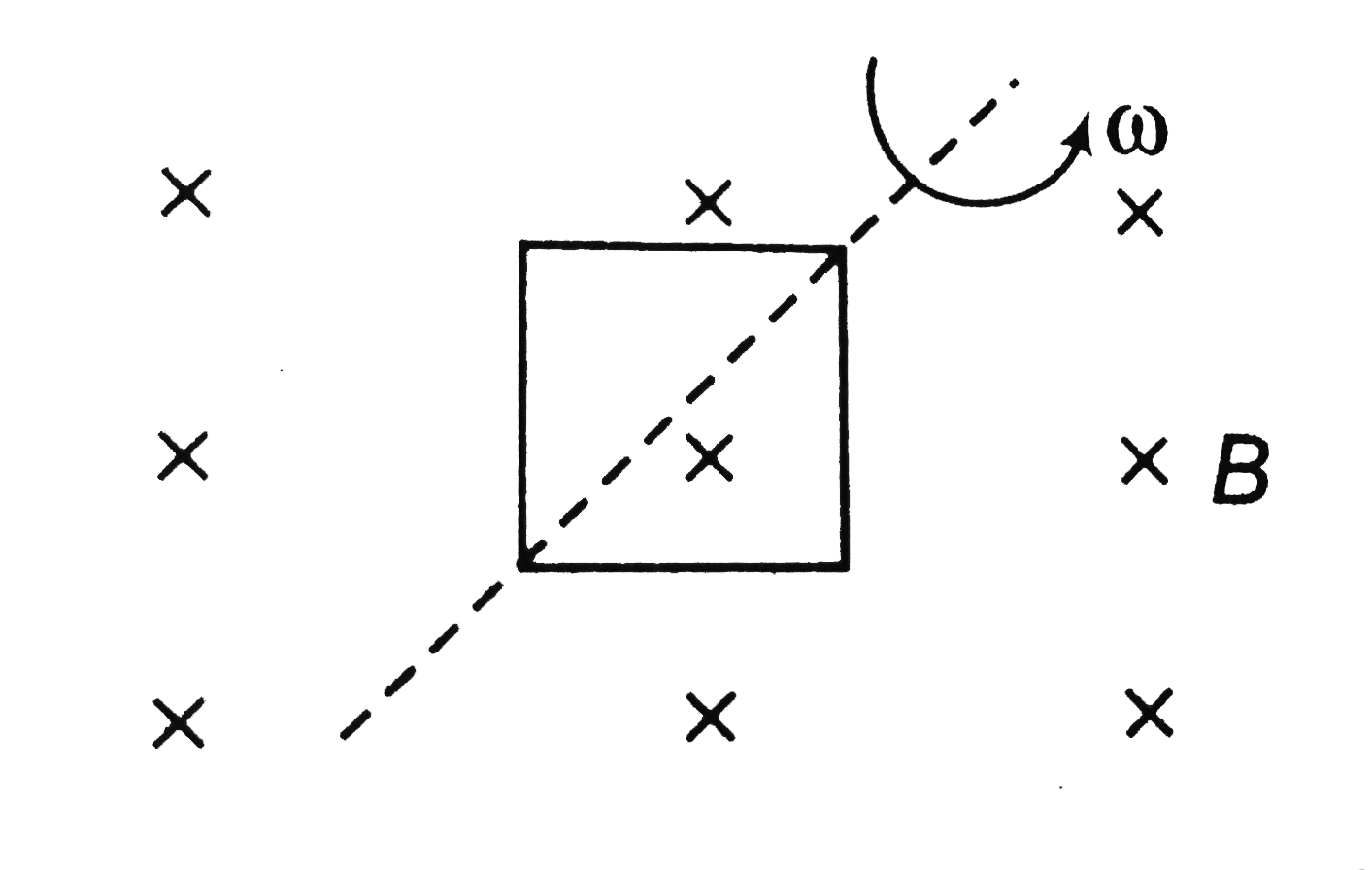 View Solution
View SolutionThe linear loop has an area of 5×10−4m2 and a resistance oof 2Ω. The larger circular loop is fixed and has a radius of 0.1m. Both the loops are concentric and coplanner. The smaller loop is rotated with an angular velocity ωrads−1 about its dismeter. The magnetic flux with the smaller loop is
 View Solution
View SolutionA small circular loop of wire of radius a is located at the centre of a much larger circular wire loop of radius b. The two loops are in the same plane. The outer loop of radius b carries an alternating current I=I0cos(ωt). The emf induced in the smaller inner loop is nearly ?
View SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 90^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View SolutionA wire loop enclosing a semi-circle of radius a=2cm is located on the boundary of a uniform magnetic field of induction B=1T (figure).At the moment t=0 the loop is set into rotation with a constant angular acceleration β=2rad/sec2 about an axis O coinciding with a line of vector B on the boundary.The emf induced in the loop as a function of time t is [x×10−4(−1)n×t]V, where n=1,2,... is the number of the half-revolution taht the loop performs at the given moment t.Find the value of x.(The arrow in the figure shows the emf direction taken to be positive, at t=0 loop was completely outside)
 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
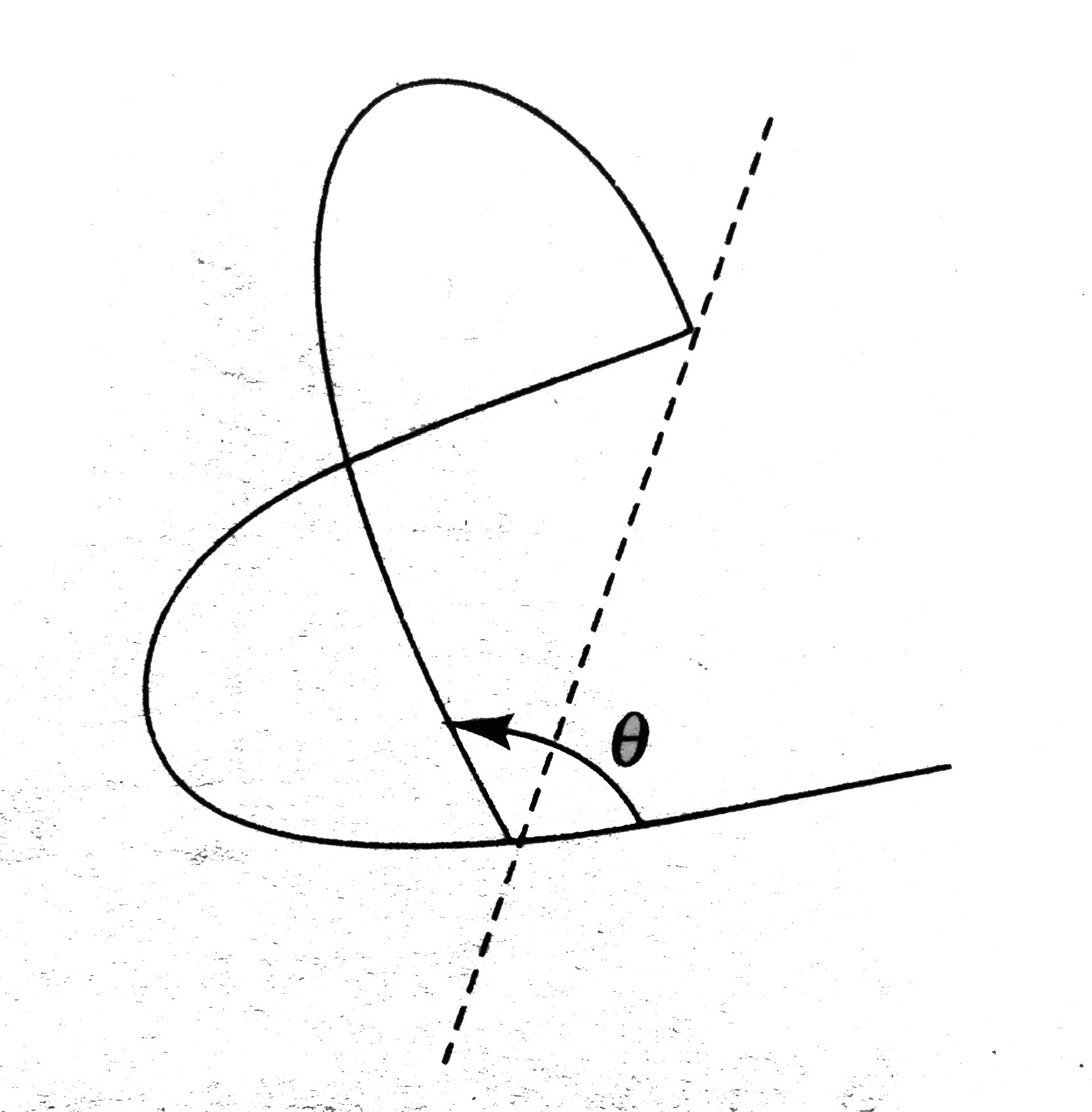 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
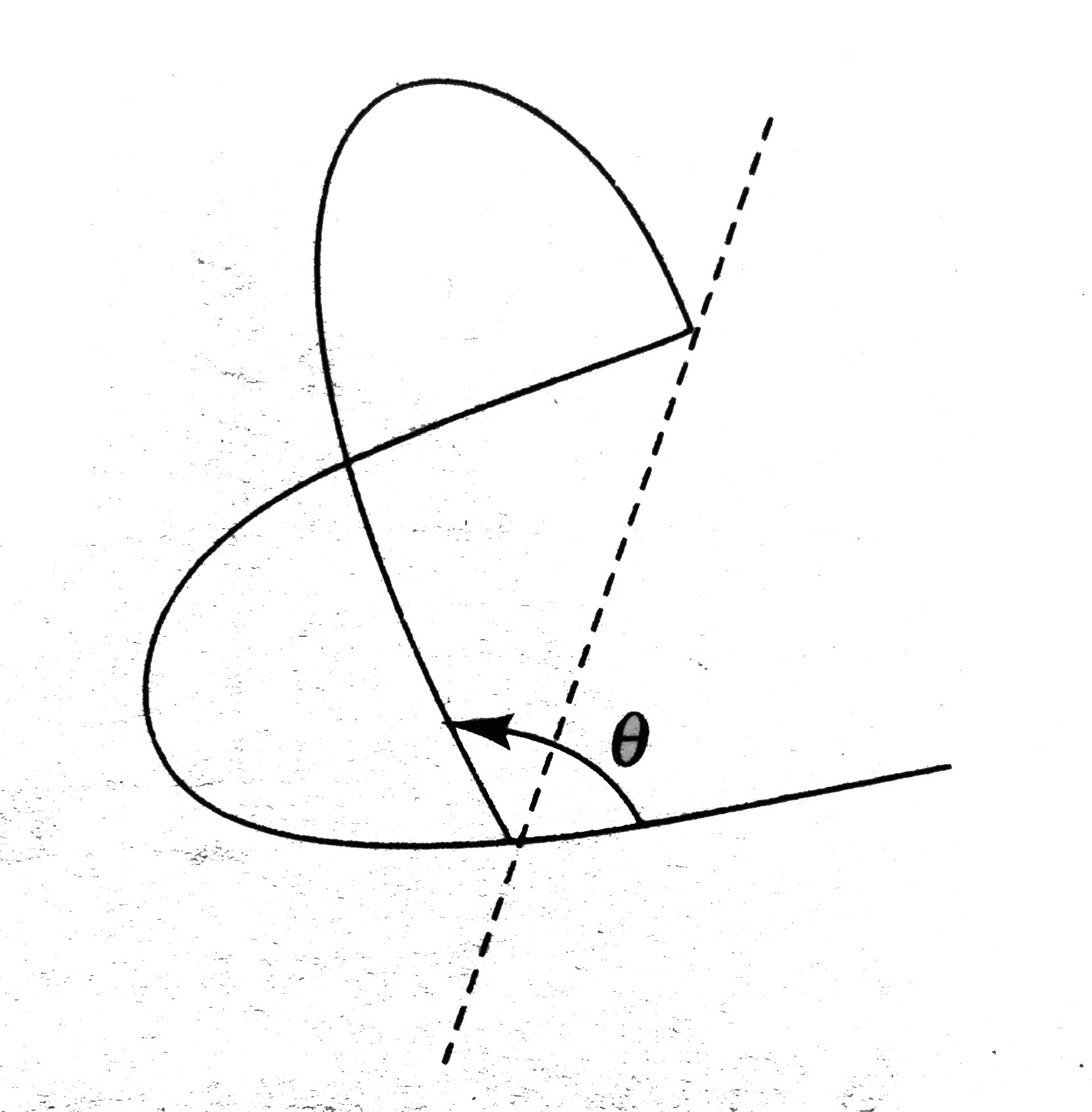 View Solution
View SolutionA circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>> r) carrying a current I. The plane of the smaller loop makes an angle of 30∘ with that of the larger loop. It the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
View Solution


