Assertion If two inductors are in paralled, then current in distributes in inverse ratio of their inductance.
Reason In parallel, potential difference remains constant.
If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:A
To solve the question regarding the assertion and reason about inductors in parallel, we will break it down step by step.
1. Understanding the Assertion:
- The assertion states that if two inductors are in parallel, the current through each inductor distributes in the inverse ratio of their inductances. This means if we have two inductors with inductances L1 and L2, the currents I1 and I2 through them will satisfy the relationship:
I1I2=L2L1
2. Understanding the Reason:
- The reason provided states that in a parallel circuit, the potential difference (voltage) across each component remains constant. This is a fundamental property of parallel circuits.
3. Applying the Formula for Inductors:
- For an inductor, the voltage V across it is related to the inductance L and the rate of change of current I through it by the formula:
V=LdIdt
- Since the inductors are in parallel, the voltage across both inductors is the same. Therefore, we can set up the equations for both inductors:
V=L1dI1dt=L2dI2dt
4. Relating Currents and Inductances:
- Since the voltage V is constant, we can express the change in current as:
L1dI1dt=L2dI2dt
- Rearranging gives us:
dI1dI2=L2L1
- This shows that the currents through the inductors are indeed in the inverse ratio of their inductances, confirming the assertion.
5. Conclusion:
- Both the assertion and the reason are correct. The reason correctly explains why the current divides in the manner described in the assertion.
Final Answer:
- Assertion: True
- Reason: True
- Therefore, the correct option is that both the assertion and reason are correct, and the reason is the correct explanation for the assertion.
---
- The assertion states that if two inductors are in parallel, the current through each inductor distributes in the inverse ratio of their inductances. This means if we have two inductors with inductances L1 and L2, the currents I1 and I2 through them will satisfy the relationship:
I1I2=L2L1
- The reason provided states that in a parallel circuit, the potential difference (voltage) across each component remains constant. This is a fundamental property of parallel circuits.
- For an inductor, the voltage V across it is related to the inductance L and the rate of change of current I through it by the formula:
V=LdIdt
- Since the inductors are in parallel, the voltage across both inductors is the same. Therefore, we can set up the equations for both inductors:
V=L1dI1dt=L2dI2dt
- Since the voltage V is constant, we can express the change in current as:
L1dI1dt=L2dI2dt
- Rearranging gives us:
dI1dI2=L2L1
- This shows that the currents through the inductors are indeed in the inverse ratio of their inductances, confirming the assertion.
- Both the assertion and the reason are correct. The reason correctly explains why the current divides in the manner described in the assertion.
- Assertion: True
- Reason: True
- Therefore, the correct option is that both the assertion and reason are correct, and the reason is the correct explanation for the assertion.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Assertion : In parallel, current distributes in inverse ratio of inductance . i∝1L
Reason : In electrical circuits, an inductor can be treated as a resistor.
View SolutionIn series, potential difference distributes in direct ratio of resistance and in parallel current is distributed in inverse ratio of resistance
In the circuit shown in figure

View Solution
Knowledge Check
Assertion : The inductive reactance limits amplitude of the current in a purely inductive circuit.
Reason : The inductive reactance is independent of the frequency of the current.AIf both assertion ans reason are true ans reaason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion istrue but reason is false.DIf both assertion and reason are false.Assertion : The interference of two identical waves moving in same direction produces standing waves.
Reason : Various elements of standing waves do not remain in constant phase.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
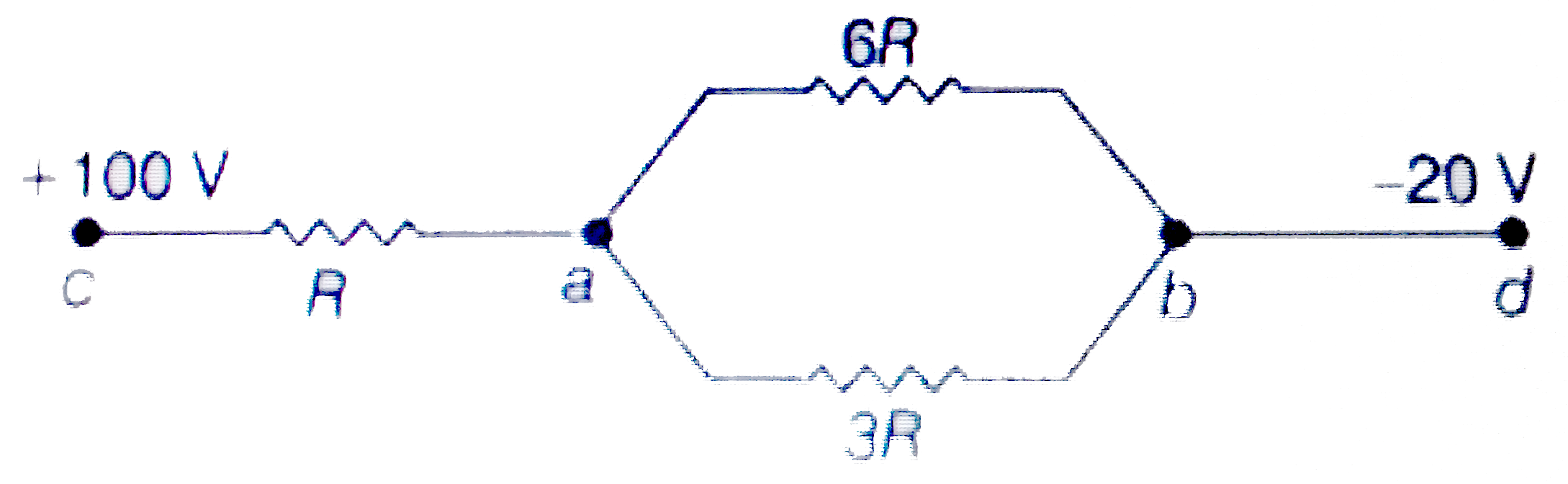
In series, potential difference distributes in direct ratio of resistance and in parallel current is distributed in inverse ratio of resistance
Ratio of current through R, 6R and 3R will be
View SolutionAssertion: Two capacitors are connected in series with a battery. Energy stored across them is in inverse ratio of their capacity.
Reason: U=12qV or U∝qV
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View SolutionA condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor wehnn the potential difference across the condenser reduces to V2 is
View SolutionAssertion : The size and shape of the rigid body remains unaffected under the effect of external force.
Reason : The distance between two particles remains constant in a rigid body.
View Solution
