Assertion : In parallel, current distributes in inverse ratio of inductance . i∝1L
Reason : In electrical circuits, an inductor can be treated as a resistor.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:C
To solve the given problem, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that "In parallel, current distributes in inverse ratio of inductance."
- When two or more inductors are connected in parallel, the voltage across each inductor is the same. According to the formula for inductors, the voltage V across an inductor is given by:
V=Ldidt
- For two inductors L1 and L2 connected in parallel, we can write:
V=L1di1dt=L2di2dt
- Since the voltages are equal, we can equate the two expressions:
L1di1dt=L2di2dt
- Rearranging gives us:
L1L2=di2di1
- This shows that the current through each inductor is inversely proportional to its inductance. Therefore, the assertion is true.
Step 2: Analyze the Reason
The reason states that "In electrical circuits, an inductor can be treated as a resistor."
- This statement is false. An inductor and a resistor have fundamentally different properties.
- An inductor stores energy in the form of a magnetic field when current flows through it, while a resistor dissipates energy as heat.
- Additionally, an inductor opposes changes in current due to its inductance, which is not a property of resistors. Therefore, the reason is false.
Conclusion
- The assertion is true, while the reason is false. Thus, the correct answer is that the assertion is true and the reason is false.
Final Answer
Assertion is true; Reason is false.
---
The assertion states that "In parallel, current distributes in inverse ratio of inductance."
V=Ldidt
- For two inductors L1 and L2 connected in parallel, we can write:
V=L1di1dt=L2di2dt
- Since the voltages are equal, we can equate the two expressions:
L1di1dt=L2di2dt
- Rearranging gives us:
L1L2=di2di1
- This shows that the current through each inductor is inversely proportional to its inductance. Therefore, the assertion is true.
The reason states that "In electrical circuits, an inductor can be treated as a resistor."
- An inductor stores energy in the form of a magnetic field when current flows through it, while a resistor dissipates energy as heat.
- Additionally, an inductor opposes changes in current due to its inductance, which is not a property of resistors. Therefore, the reason is false.
- The assertion is true, while the reason is false. Thus, the correct answer is that the assertion is true and the reason is false.
Assertion is true; Reason is false.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Objective
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.7
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Assertion If two inductors are in paralled, then current in distributes in inverse ratio of their inductance.
Reason In parallel, potential difference remains constant.
View SolutionIn an electric circuit shown alongside, find
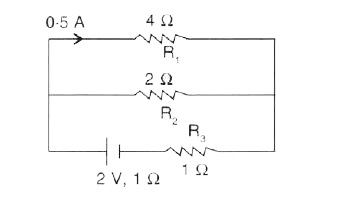
current in resistor 1Ω
View SolutionIn series, potential difference distributes in direct ratio of resistance and in parallel current is distributed in inverse ratio of resistance
Ratio of current through R, 6R and 3R will be
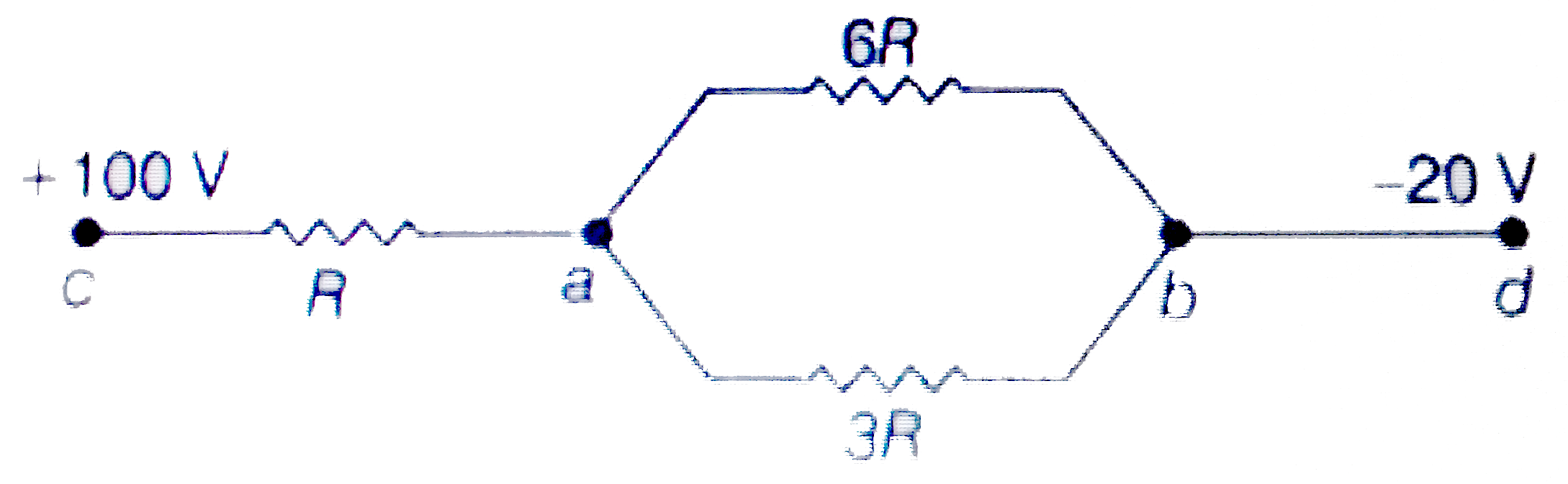
View SolutionIn series, potential difference distributes in direct ratio of resistance and in parallel current is distributed in inverse ratio of resistance
In the circuit shown in figure

View SolutionAssertion: In the circuit in figure, time constant of charging of capacitor is sCR2
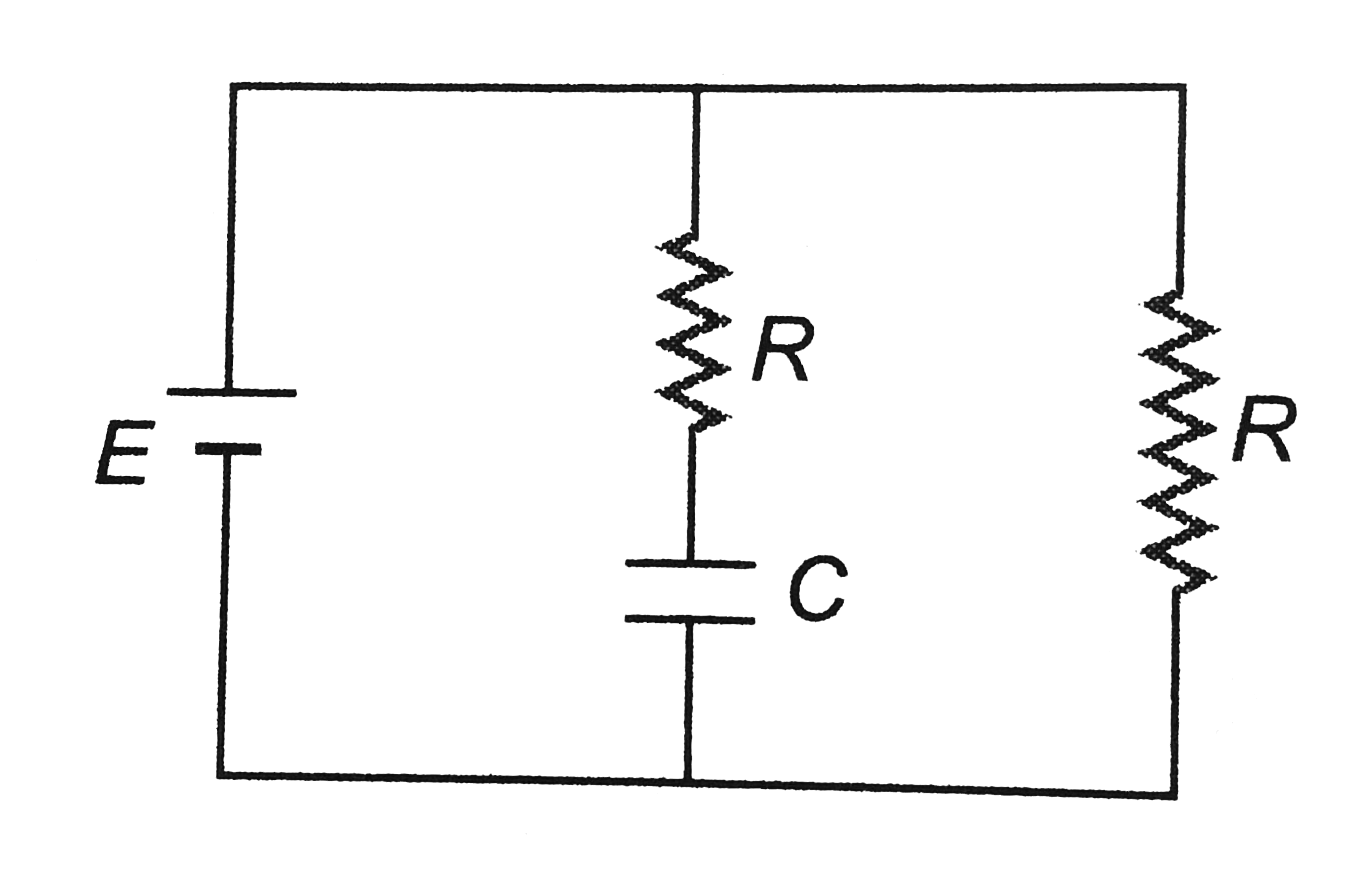
Reason: In the absence of capcitor in the circuit, two resistors are in parallel with the battery.
View SolutionAssertion : In series L−C−R circuit, if a ferromagnetic rod is inserted inside an inductor, current in the circuit may increase or decrease.
Reason : By doing so XL will increase.
View Solution(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent
resistance of a group of resistances joined in parallel is equal to the sum of the
reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12Ω each are joined in parallel to a 6V battery.
Find the current drawn from the battery.
View SolutionAssertion: Inductive reactance of an inductor in DC circuit is zero.
Reason: Angular frequency of DC circuit is zero.
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
View SolutionAssertion: The alternating current lags behined the e.m.f. by a phase angle of π/2, when AC flows through an inductor.
Reason: The inductive reactance increases as the frequency of AC source decreases.
View Solution
