Assertion Coefficient of self-induction of an inductor depends upon the rate of change of current passing through it.
Reason From, e=−Ldidt
We can see that, L=−e(di/dt)orL∝1(di/dt)
If both Assertion and Reason are corrent and Reason is the corrent explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is ture.
The correct Answer is:D
To solve the given question, we need to analyze the assertion and the reason provided regarding the coefficient of self-induction of an inductor.
1. Understanding the Assertion:
- The assertion states that the coefficient of self-induction (L) of an inductor depends upon the rate of change of current passing through it.
- This implies that as the rate of change of current increases, the self-inductance would also change.
2. Understanding the Reason:
- The reason states that according to the formula e=−Ldidt, where e is the induced electromotive force (emf), L is the self-inductance, and didt is the rate of change of current.
- Rearranging this gives L=−edidt, suggesting that L is inversely proportional to the rate of change of current when the induced emf is constant.
3. Analyzing the Relationship:
- The coefficient of self-inductance L is a property of the inductor itself, determined by its physical characteristics (number of turns, area of the coil, and length of the coil).
- It does not change with the rate of change of current; rather, it remains constant for a given inductor.
4. Conclusion on Assertion and Reason:
- The assertion is false because the coefficient of self-inductance does not depend on the rate of change of current.
- The reason is true as it correctly describes the relationship between induced emf and the rate of change of current.
5. Final Answer:
- The assertion is false, and the reason is true. Therefore, the correct option is D.
- The assertion states that the coefficient of self-induction (L) of an inductor depends upon the rate of change of current passing through it.
- This implies that as the rate of change of current increases, the self-inductance would also change.
- The reason states that according to the formula e=−Ldidt, where e is the induced electromotive force (emf), L is the self-inductance, and didt is the rate of change of current.
- Rearranging this gives L=−edidt, suggesting that L is inversely proportional to the rate of change of current when the induced emf is constant.
- The coefficient of self-inductance L is a property of the inductor itself, determined by its physical characteristics (number of turns, area of the coil, and length of the coil).
- It does not change with the rate of change of current; rather, it remains constant for a given inductor.
- The assertion is false because the coefficient of self-inductance does not depend on the rate of change of current.
- The reason is true as it correctly describes the relationship between induced emf and the rate of change of current.
- The assertion is false, and the reason is true. Therefore, the correct option is D.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A battery of emf E and of negligible internal resistance is connected in a L−R circuit as shown in figure. The inductor has a piece of soft iron inside it. When steady state is reached in the piece of soft iron is abruptly pulled out suddenly so that the inductance of the inductor decreases to nL with n<1 with battery remaining connected. Calculate.
a. Current as a function of time assuming t=0 at the instant when piece is pulled.
b. the work done to pull out the piece.
c. thermal power generated in the circuit as as function of time.
d. power supplied by the battery as a function of time.
HOW TO PROCEED When the inductance of an inductor is abruptly changed, the flux passing through it remains constant.
ϕ= constant
∴Li= constant (L=ϕi)
View SolutionAssertion : Angular frequency of LC oscillations is 2rad/s and maximum current in the circuit is 1A. Then, maximum rate of change of current should be 2A/s.
Reason: (dIdt)max=(Imax)ω
View Solution
Knowledge Check
In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1s
The current through two inductors of self inductance 12 mH and 30 mH is increasing with time at the same rate. Draw graphs showing the variation of the (a ) e.m.f. induced with the rate of change of current in each inductor. (b) enargy stored in each inductor with the current flowing through it.
Compare the energy stored in the coils if power dissipated in the coil is same.
View SolutionObtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.
View SolutionSpherical rain drop evaporates at a rate proportional to its surface area. The differential equation corresponding to the rate of change of the radius of the rain drop if the constant of proportionality is K>0 is (a) (b)(c)(d)(e)dyf((g)dt)(h)(i)+K=0(j) (k) (b) (l)(m)(n)(o)drp((q)dt)(r)(s)−K=0(t) (u) (c) (d)(e)(f)(g)drh((i)dt)(j)(k)=Kr(l) (m) (d) None of these
View SolutionAssertion An induced emf of 2 V is developed in a circular loop, if current in the loop is changed at a rate of 4 As−1 .IF 4 A of current is passed through this loop, then flux linked with this coil will be 2 Wb.
Reason Flux linked with the coil is
|ϕ|=∣∣∣edi/dt∣∣∣i
View SolutionAssertion : If some ferromagnetic substance is filled inside a solenoid, its coefficient of self induction L will increase.
Reason : By increasing the current in a coil, its coefficient of self induction L can be increased.
View SolutionThe inductor shown in figure has inducance 0.54H and carries a current in the direction shown thast is decreasing at a uniform rate didt=0.03A/s.
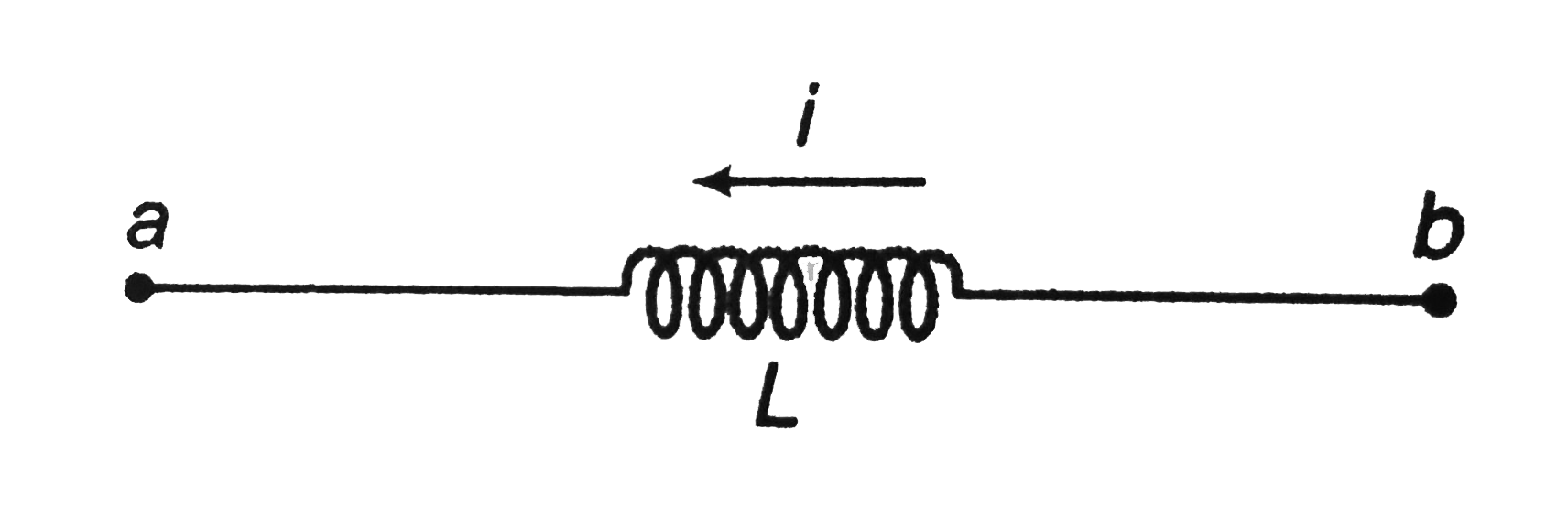
a. Find the self induced emf
b. Which emf of the inductor a ro b is at a higher potential?
View Solution
