Two identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
32po
43po
35po
2po
The correct Answer is:B
To solve the problem, we will use the ideal gas law and the concept of conservation of moles. Let's break down the solution step by step.
1. Identify the Initial Conditions:
- Both containers have the same gas with initial pressure P0 and absolute temperature T0.
- Let the volume of each container be V0.
2. Determine Moles in Each Container Initially:
- For Container 1 (maintained at T0):
n1=P0V0RT0
- For Container 2 (heated to 2T0):
n2=P0V0R(2T0)=P0V02RT0
3. Total Moles in the System:
- The total number of moles ntotal in the system is:
ntotal=n1+n2=P0V0RT0+P0V02RT0
- Simplifying this gives:
ntotal=P0V0RT0(1+12)=P0V0RT0⋅32=3P0V02RT0
4. Final Condition After Equilibrium:
- After reaching equilibrium, let the common pressure be P and the temperature of Container 1 remains T0 while Container 2 is at 2T0.
- The moles in each container at equilibrium can be expressed as:
- For Container 1:
n′1=PV0RT0
- For Container 2:
n′2=PV0R(2T0)=PV02RT0
5. Equating Total Moles:
- At equilibrium, the total moles must remain the same:
n′1+n′2=ntotal
- Substituting the expressions:
PV0RT0+PV02RT0=3P0V02RT0
6. Simplifying the Equation:
- Factor out V0RT0:
(P+P2)=3P02
- This simplifies to:
3P2=3P02
7. Solving for Common Pressure P:
- Multiply both sides by 23:
P=P0⋅43
Final Answer:
The common pressure of the gases after equilibrium is:
P=4P03
- Both containers have the same gas with initial pressure P0 and absolute temperature T0.
- Let the volume of each container be V0.
- For Container 1 (maintained at T0):
n1=P0V0RT0
- For Container 2 (heated to 2T0):
n2=P0V0R(2T0)=P0V02RT0
- The total number of moles ntotal in the system is:
ntotal=n1+n2=P0V0RT0+P0V02RT0
- Simplifying this gives:
ntotal=P0V0RT0(1+12)=P0V0RT0⋅32=3P0V02RT0
- After reaching equilibrium, let the common pressure be P and the temperature of Container 1 remains T0 while Container 2 is at 2T0.
- The moles in each container at equilibrium can be expressed as:
- For Container 1:
n′1=PV0RT0
- For Container 2:
n′2=PV0R(2T0)=PV02RT0
- At equilibrium, the total moles must remain the same:
n′1+n′2=ntotal
- Substituting the expressions:
PV0RT0+PV02RT0=3P0V02RT0
- Factor out V0RT0:
(P+P2)=3P02
- This simplifies to:
3P2=3P02
- Multiply both sides by 23:
P=P0⋅43
The common pressure of the gases after equilibrium is:
P=4P03
Topper's Solved these Questions
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - B medical entrance special format questions
14 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Match the columns
5 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Check point 14.4
25 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
Similar Questions
Assertion At the same temperature and pressure, equal volums of all gases gases contain equal numbe of molecules.
Reason In 1 L at NTP total number of molecules are 6.02×1023.
View SolutionFor a monotomic gas at temperature T, match the following columns.
ColumnIColumnII(A)Speed of sound(p)√2RT/M(B)RMS speed of gas molecules(q)√8RT/πM(C)Average speed of gas molecules(r)√3RT/M(D)Most probable speed of gas molecules(s)√5RT/3M
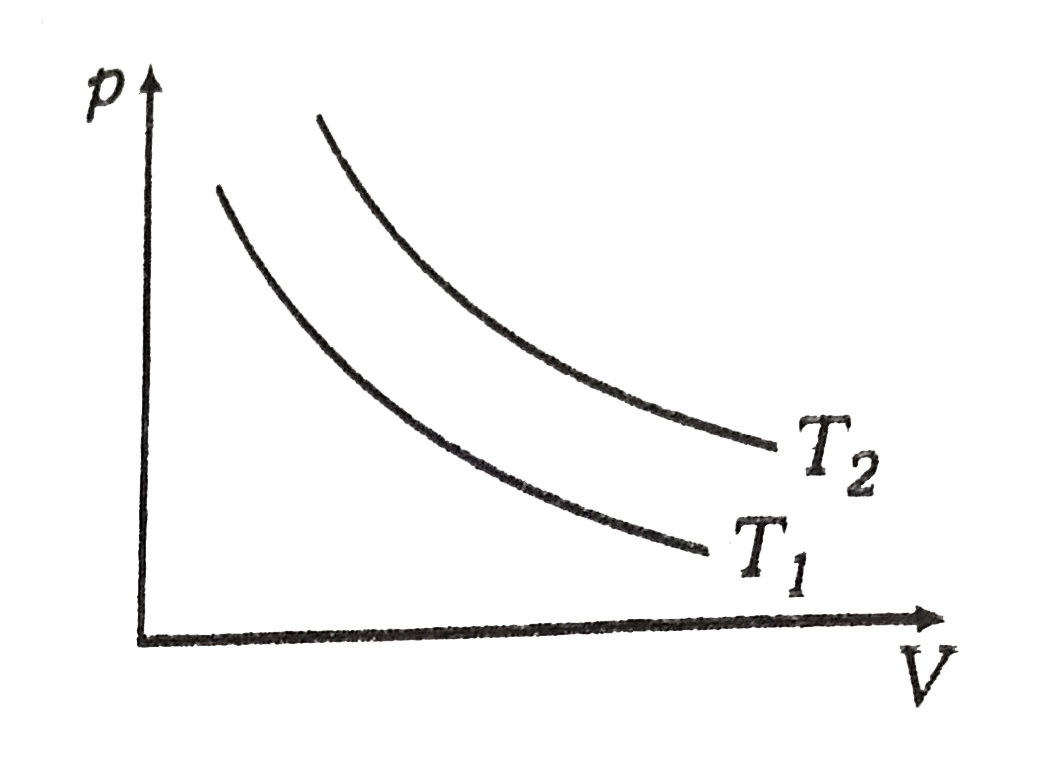
View SolutionThe adjoining fgure shows graph of pressure and volume of a gas at two temperatures T1 and T2 Which one the following is correct
View SolutionThree pieces of string, each of length L, are joined together end-to-end, to make a combined string of length 3L. The first piece of string has mass per unit length μ1, the second piece has mass per unit length μ2=4μ1 and the third piece has mass per unit length μ3=μ1/4 .
(a) If the combined string is under tension F, how much time does it take a transverse wave to travel the entire length 3L? Give your answer in terms of L,F and μ1 .
(b) Does your answer to part (a) depend on the order in which the three piece are joined together? Explain.
View SolutionShow that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
View SolutionTwo identical vessels contain the same gas at pressure P_(1) and P_(2) at absolute temperature T_(1) and T_(2) , respectively. On joining the vessels with a small tube as shown in the figure. The gas reaches a common temperature T and a common pressure P. Determine the ratio P//T
View SolutionAt the same temperature and pressure , equal volumes of different gases contain the same number of
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p_(0) and absolute temperature T_(0) . One container is now maintained at the same temperature while the other is heated to 2T_(0) . The common pressure of the gas
View SolutionTwo identical container each of volume V0 are joined by a small pipe. The containers contain identical gases at temperature T0 and pressure P0. One container is heated to temperature 2T0 while maintaining the other at the same temperature. The common pressure of the gas is P and n is the number of moles of gas in container at temperature 2T0.
View SolutionTwo closed vessels of equal volume contain air at P0 pressure, T0 temperature and are connected through a narrow tube, If one of the vessels is now maintained at T0 and other at T, what will be the pressure in the vessels?
View SolutionTwo identical vessels contain helium and hydrogen gases at same temperature, then
View SolutionTwo identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
View SolutionA cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless postion. The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is p_(o) and temperature is T_(o), atmospheric pressure is also p_(o) Now the temperature of the gas is increased to 2T_(0), the tension in the wire will be
View SolutionA container contains hydrogen gas at pressure P and temperature T. Another identical container contains helium gas at pressure 2P and temperature T//2 . The ratio of the number of molecules of the two gases is
View SolutionTwo identical containers, (each volume V_(0) ) Are connected by a small tube. Gas heating in the same characters T_(0) And pressure P_(0) But it is full. A vessel temperature 2T_(0) Is heated while the other is kept at the same temperature. Common Pressure P Heating of Gas 2T_(0) Find the number of moles in the vessel containing
View SolutionTwo containers, each of volume V_(0) , joined by a small pipe initially contain the same gas at pressure P_(0) and at absolute temperature T_(0) . One container is now maintained at the same temperature while the other is heated to 2T_(0) . Find(1) commom pressure of the gas, and(2) the number of moles of gas in the container at temperature 2T_(0)
View Solution
