A sphere of solid material of specific gravity 8 has a concentric spherical cavity and just sinks in water. The ratio of radius of cavity to that of outer radius of the sphere must be
3√32
3√52
3√72
23√7
The correct Answer is:C
Weight = upthrust
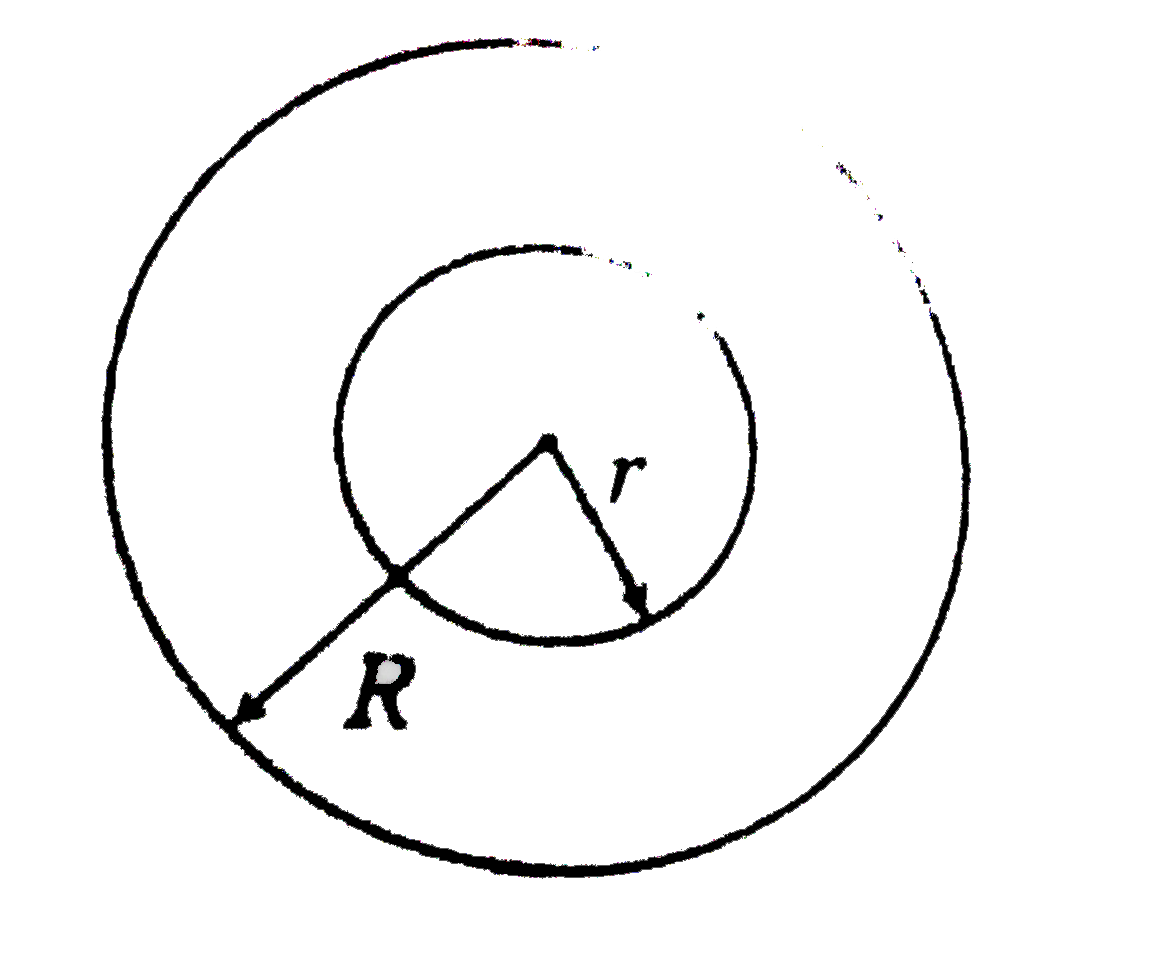
(43πR3−43πr3)(8×ρw×g)=(43πR3)ρwg
or 8R3−8r3=R3
∴ 8r3=7R3 orrR=(78)1/3=3√72
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A solid ball of metal has a concentric spherical cavity within it. If the ball is heated, the volume of the cavity will
View SolutionA sphere of radius R and made of material of relative density σ has a concentric cavity of radius r. It just floats when placed in a tank full of water. The value of the ratio R/r will be
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
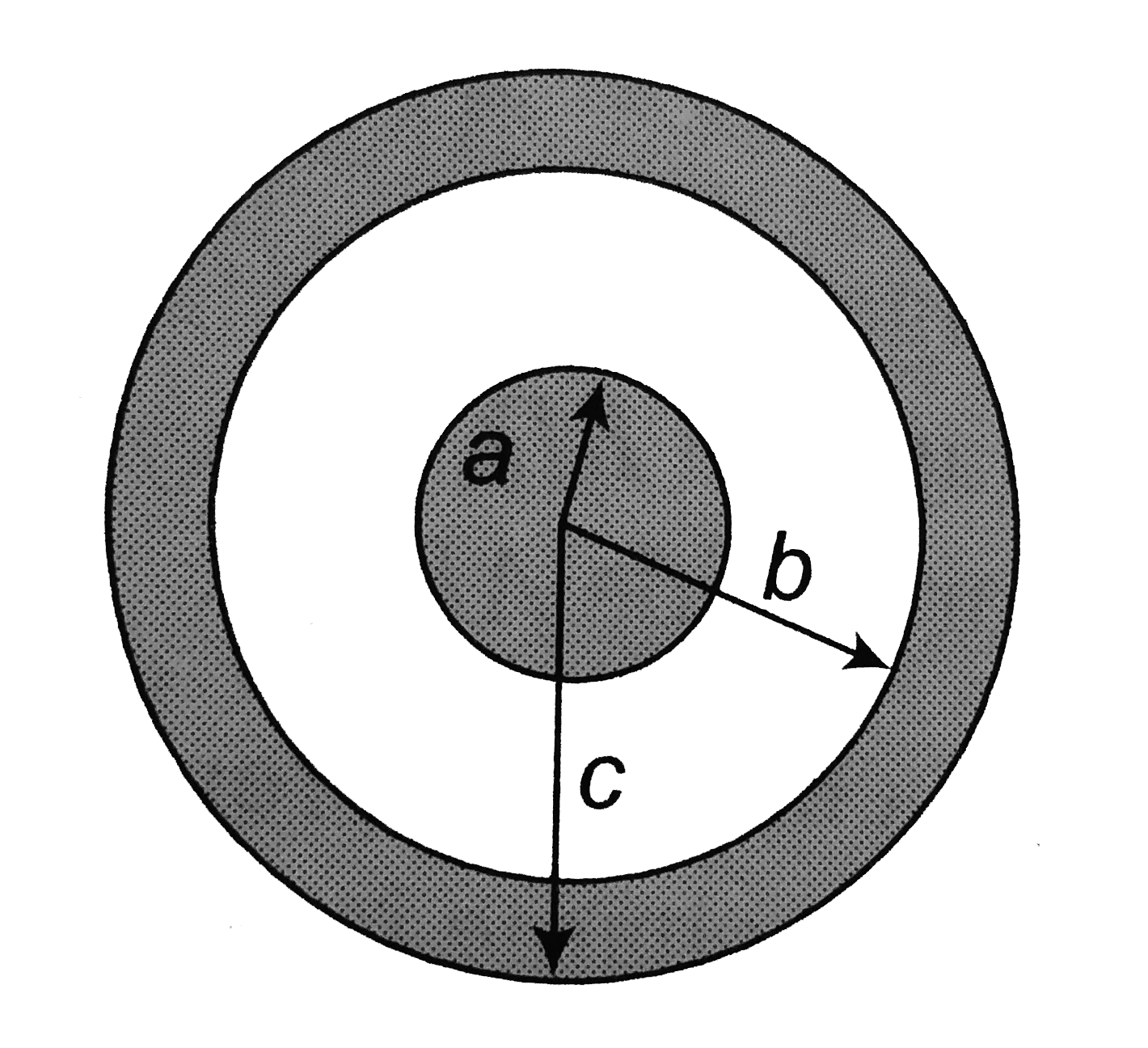
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

View Solution
