Figure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
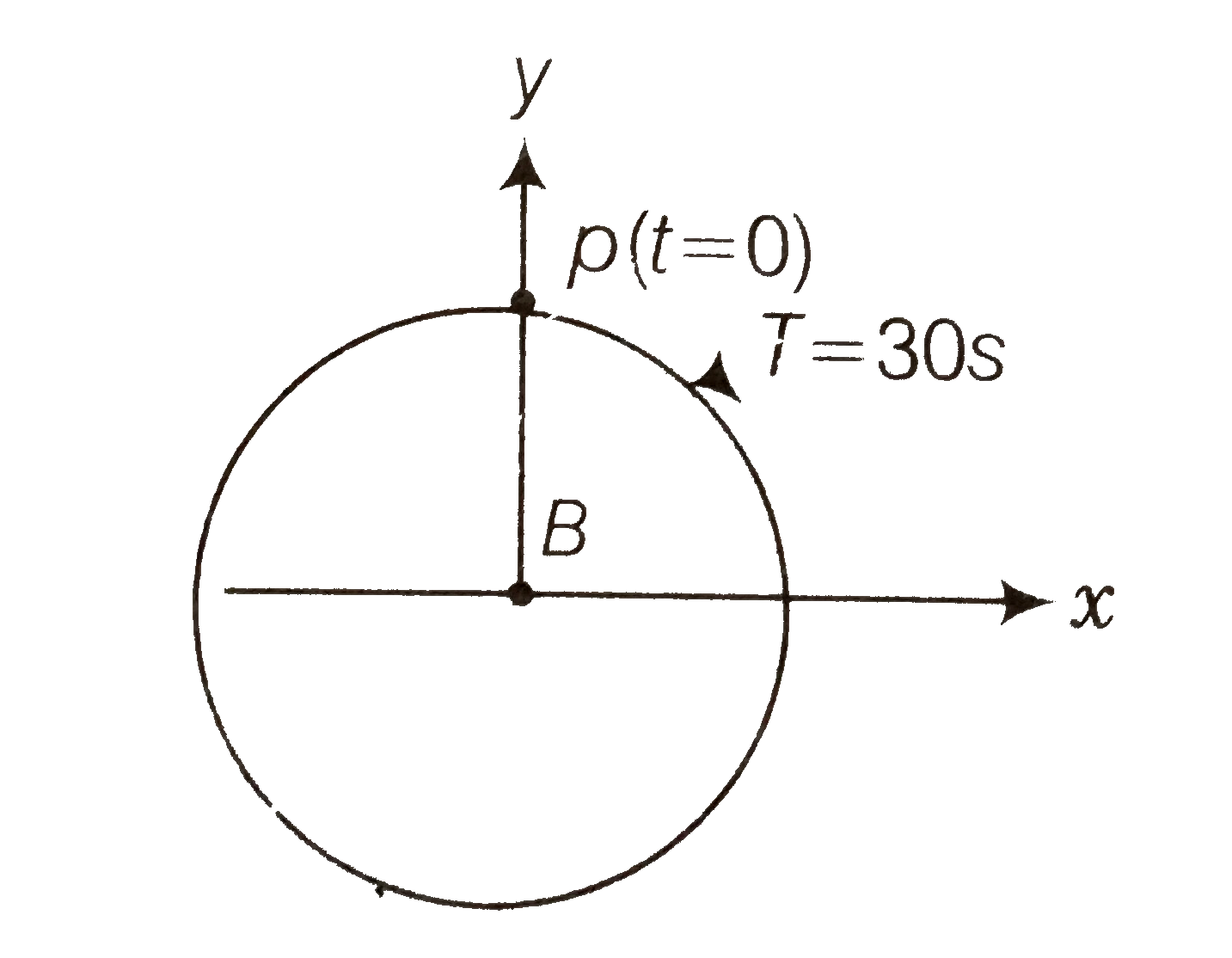
x(t)=B sin(2πt30)
x(t)=B cos(πt15)
x(t)=Bsin(π15+π2)
x(t)=Bcos(πt15+π2)
The correct Answer is:A
(a) Let angular velocity of the particle executing circular motion is ω and when it is at Q makes and angle θ as shown in the diagram.
Clearly , θ=ωt
Now, we can write OR
=OQcos(90−θ)=OQsinθ=OQsinωt
=rsinωt [∵OQ=r]
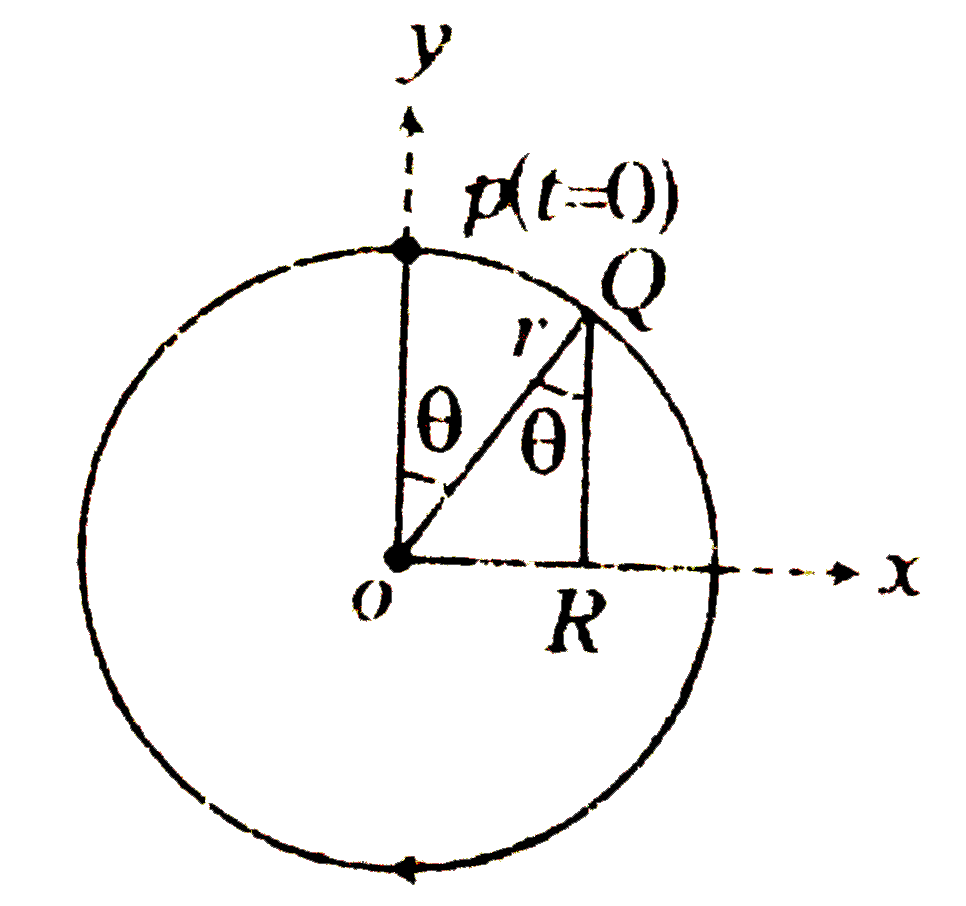
⇒x=rsinωt=Bsinωt [∵r=B]
=Bsin2πTt=Bsin(2π30t)
Clearly, this equation represents SHM.
Similar Questions
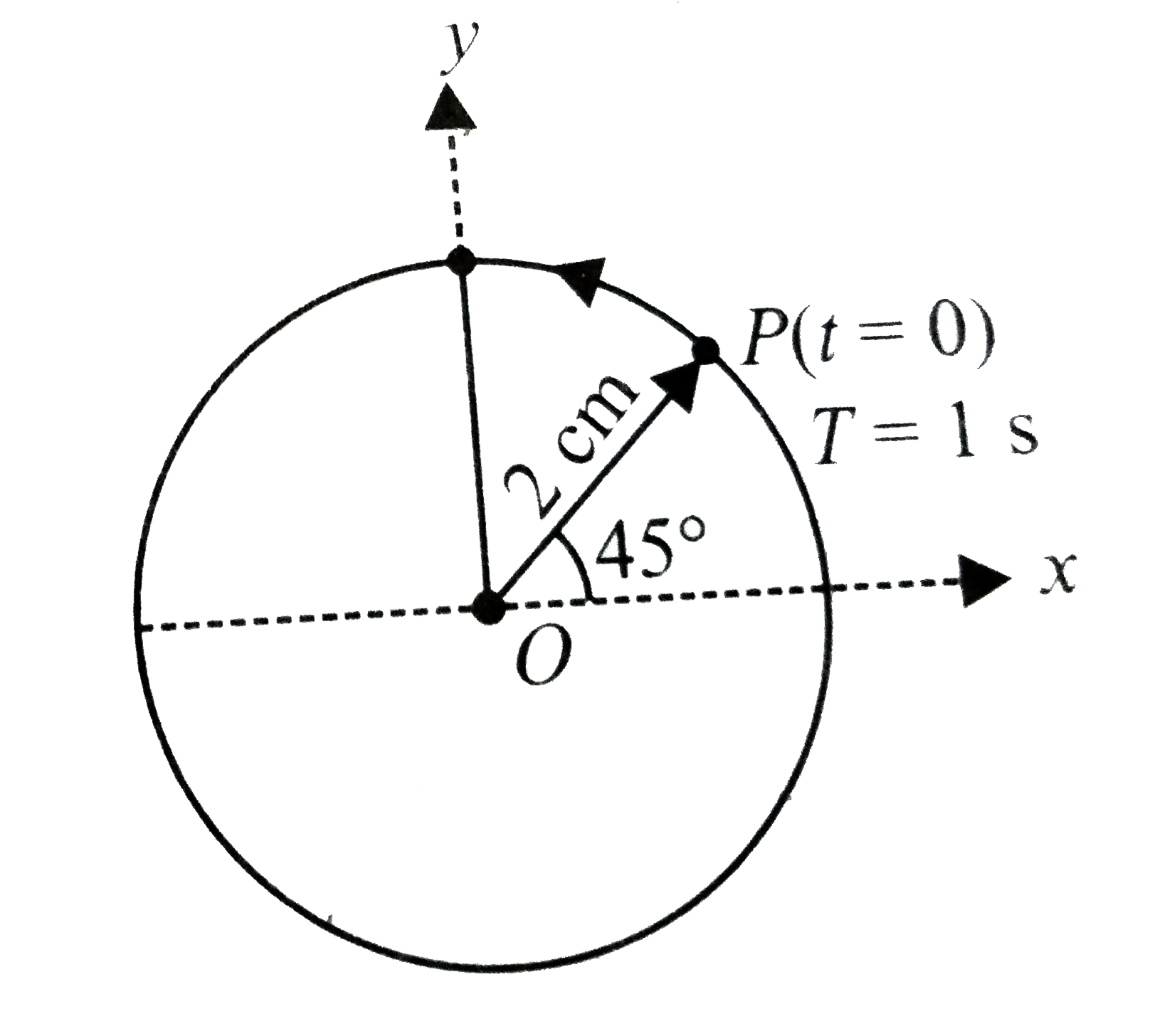
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
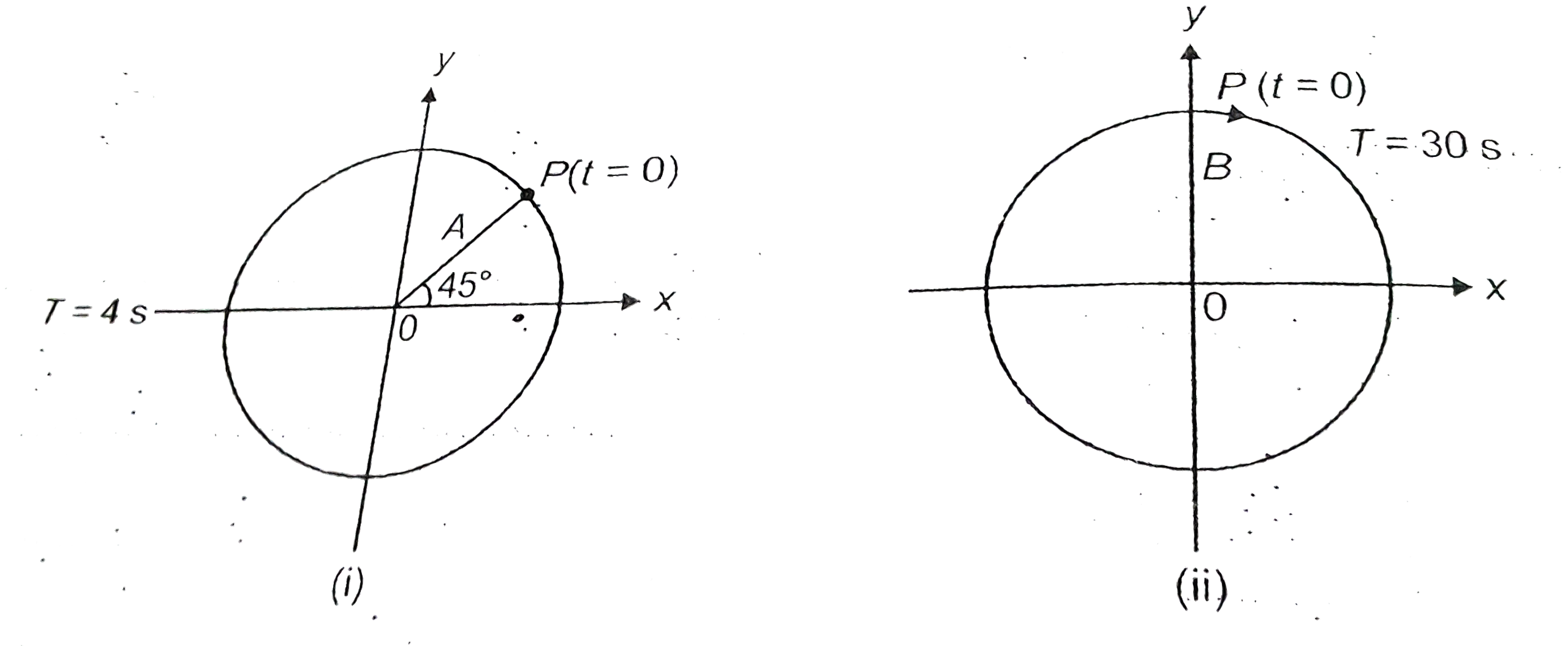
View SolutionThe following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
View Solution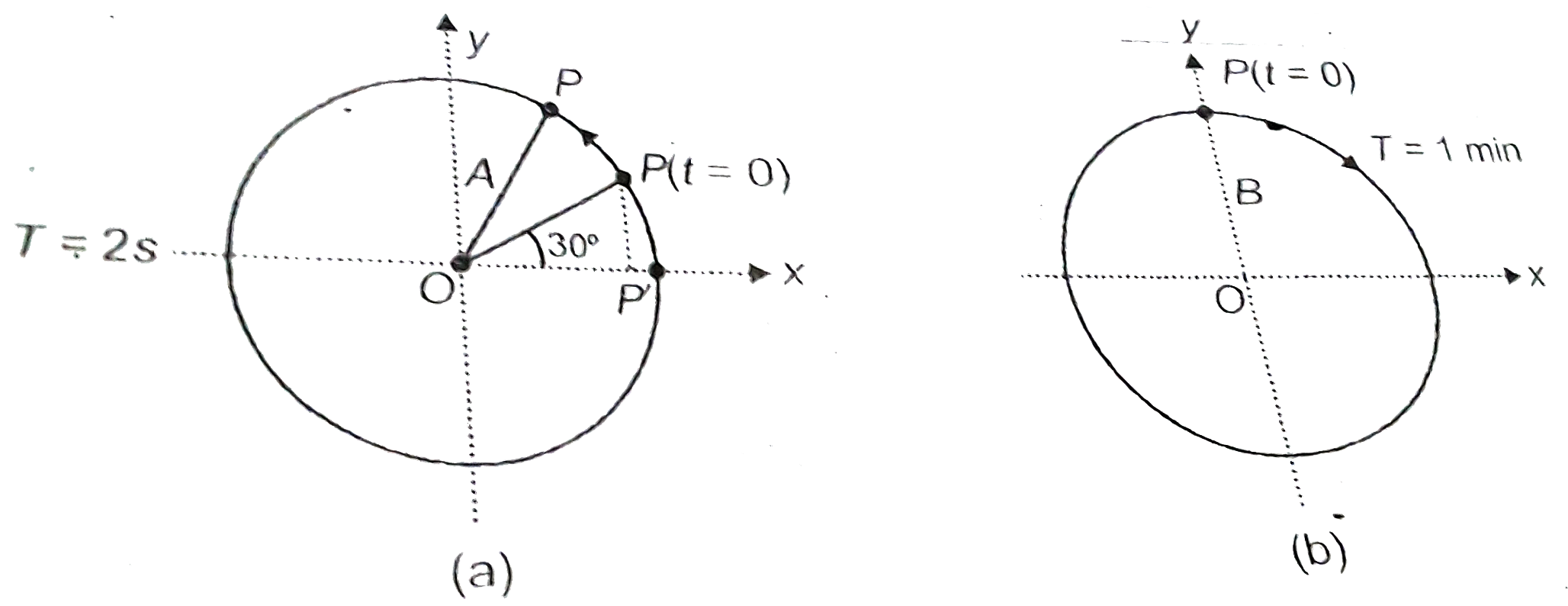
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionThe radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.

y-projection of the radius vector of rotating particle P is :
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
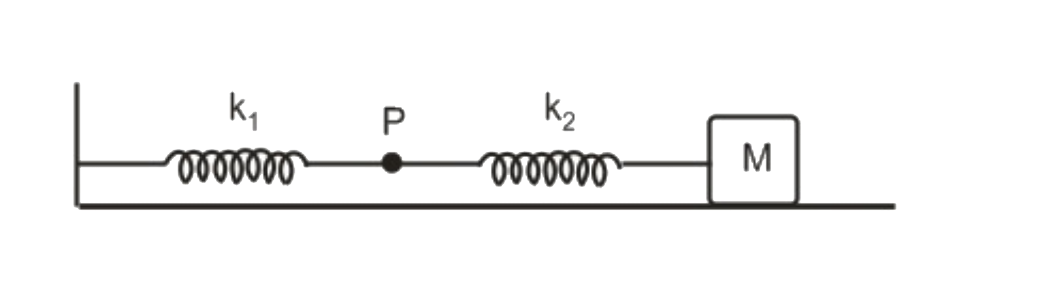
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
View SolutionThe distance moved by a particle in simple harmonic motion in one time period is
View SolutionThe shape of graph plotted between velocity and position of a particle executing simple harmonic motion is
View SolutionAs shown in figure in a simple harmonic motion oscillator having identical four springs has time period

View Solution
Figure. Shows the variation of force acting on a particle of mass 400 g executing simple harmonic motion. The frequency of oscillation of the particle is
View Solution