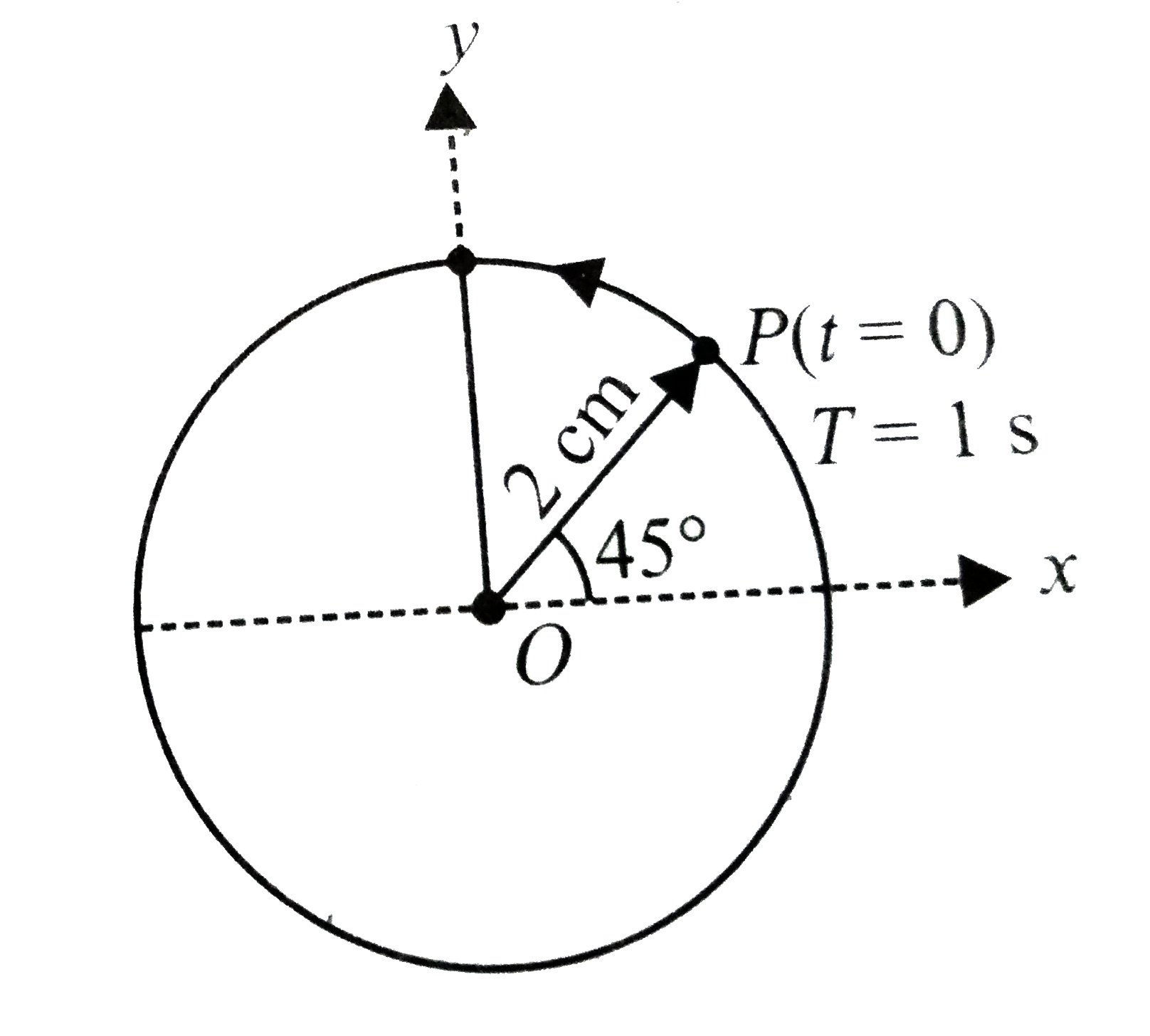
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
x=2cos(2πt+π4)
x=2sin(2πt+π4)
x=2sin(2πt−π4)
x=2cos(2πt−π4)
The correct Answer is:A
Here, T=1s
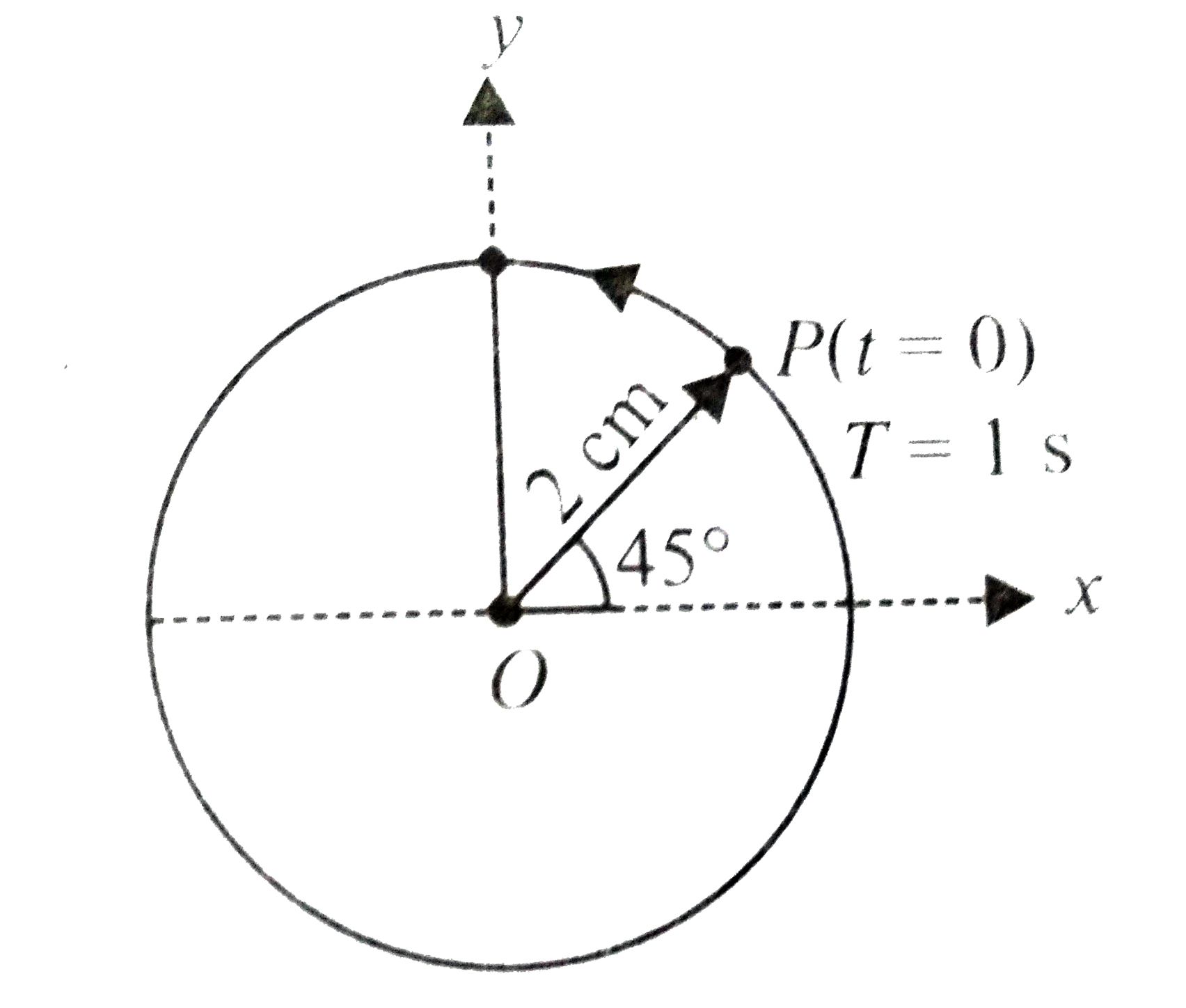
At t=0, OP makes an π4(=45∘) with the x-axis
after a time, it covers an angle of 2πTt in the anticlockwise sense and makes an angle of (2πTt+π4)
with the x-axis
The projection of OP on the x-axis at time t is given by
x=2cos(2πTt+π4)
For, T=1s
∴x=2cos(2πt+π4)
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Velocity And Acceleration In Simple Harmonic Motion
18 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Force Law For Simple Harmonic Motion
2 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Simple Harmonic Motion
17 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
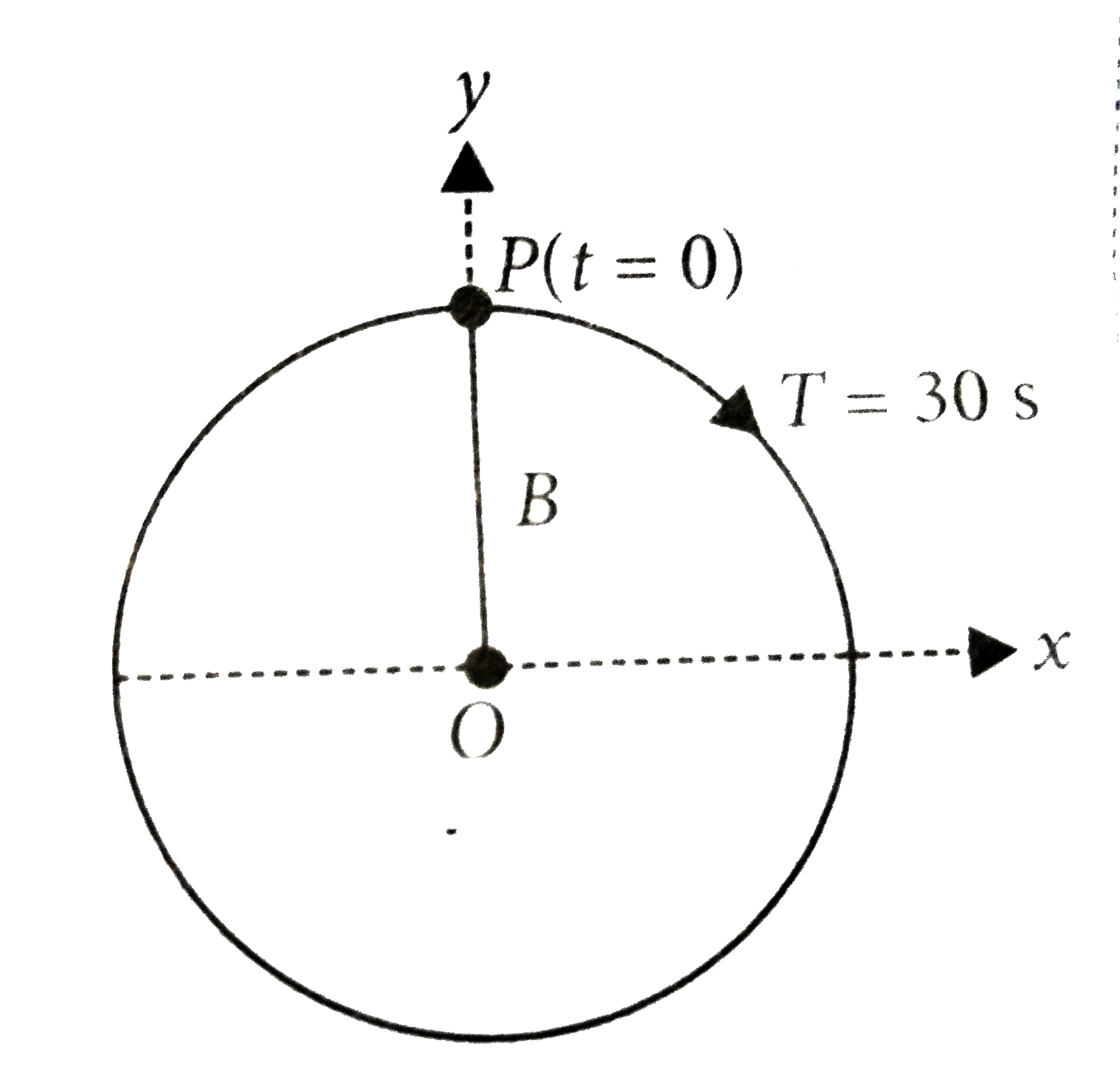
Figure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
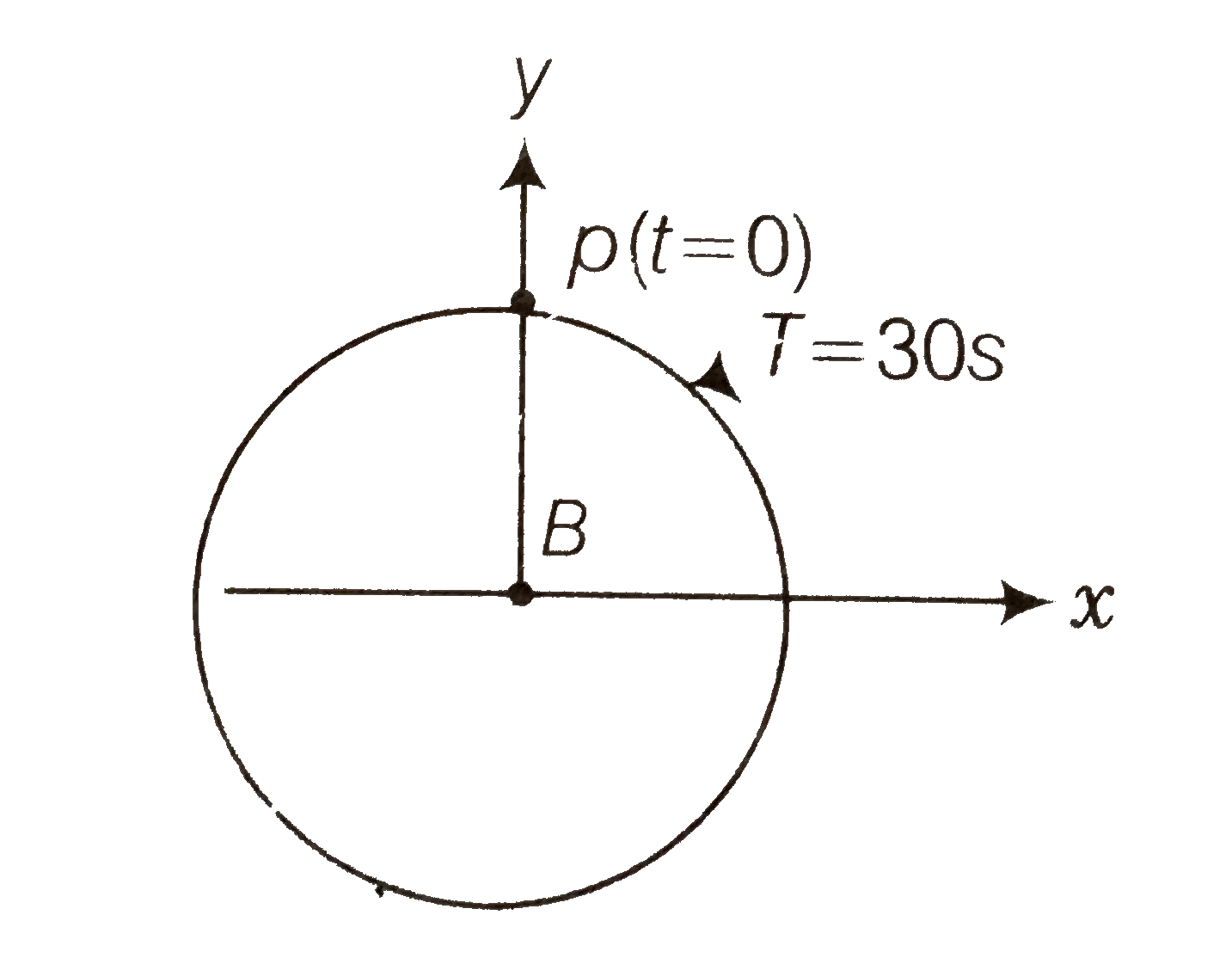
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
View SolutionThe following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
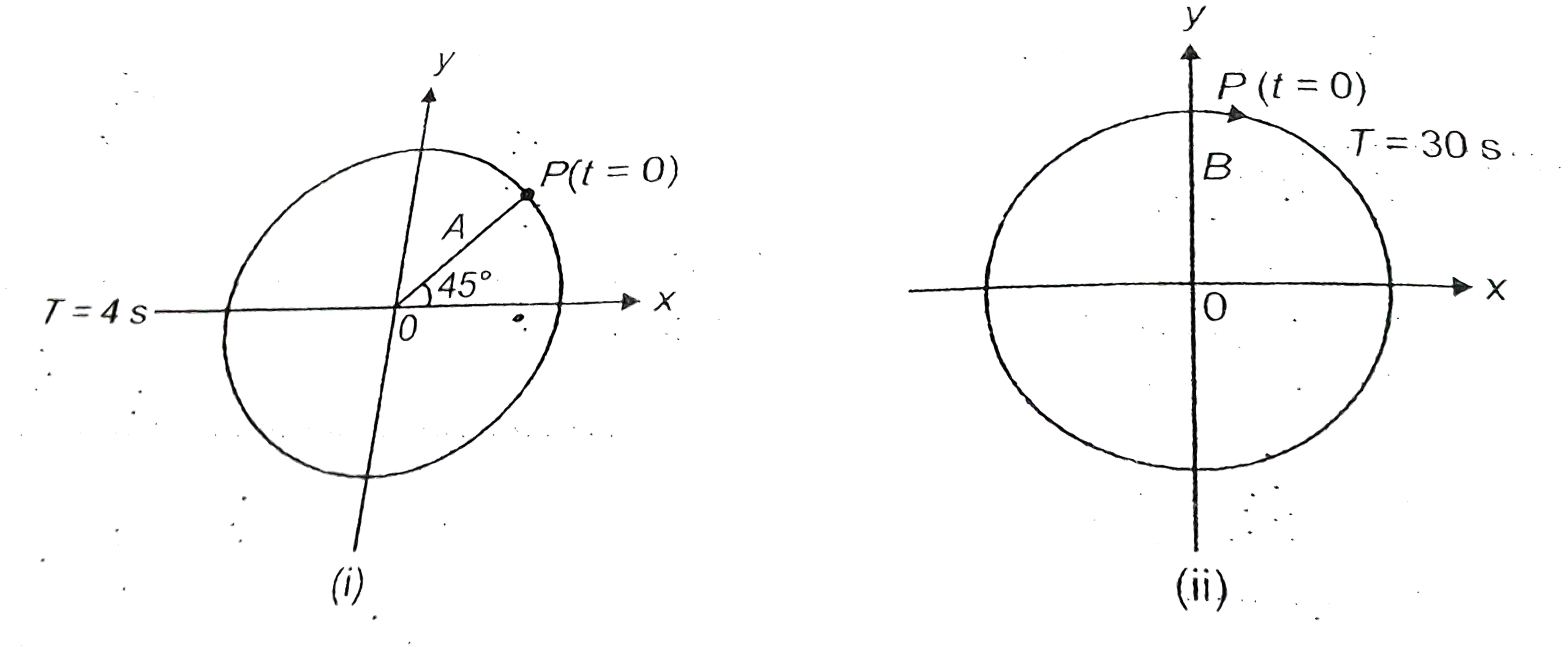
View Solution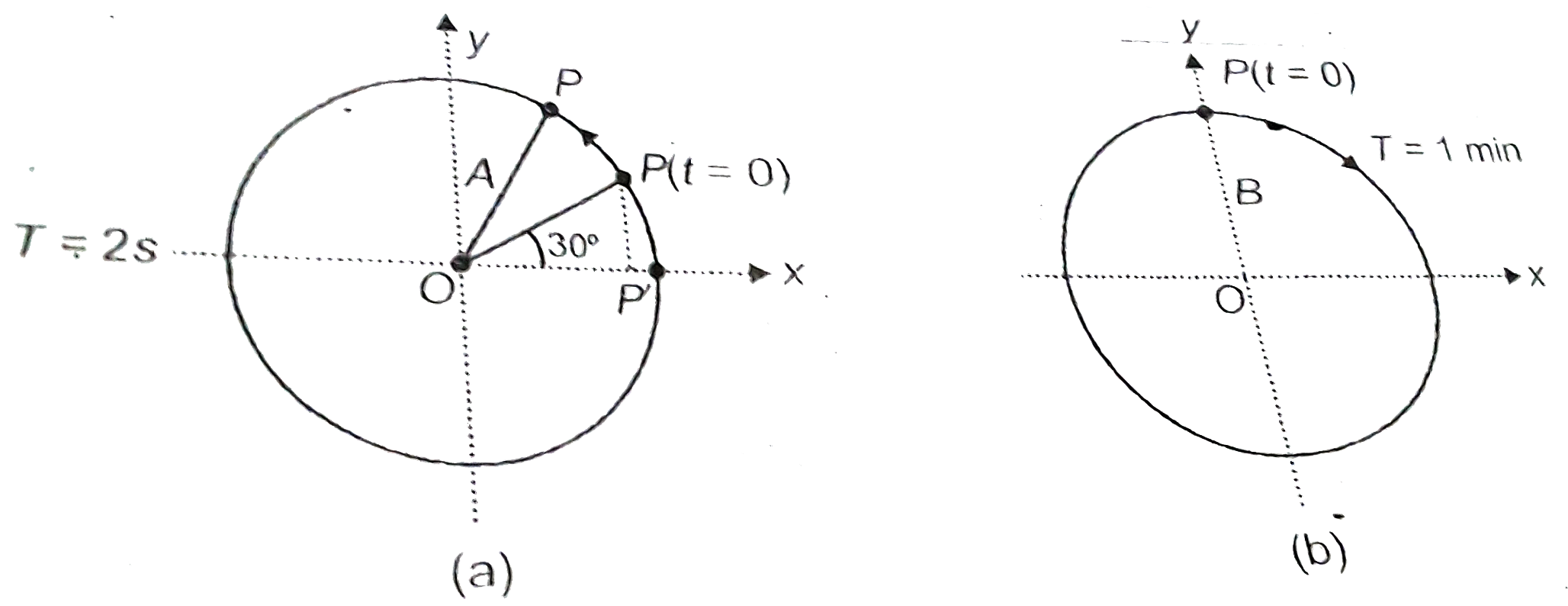
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionThe radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.
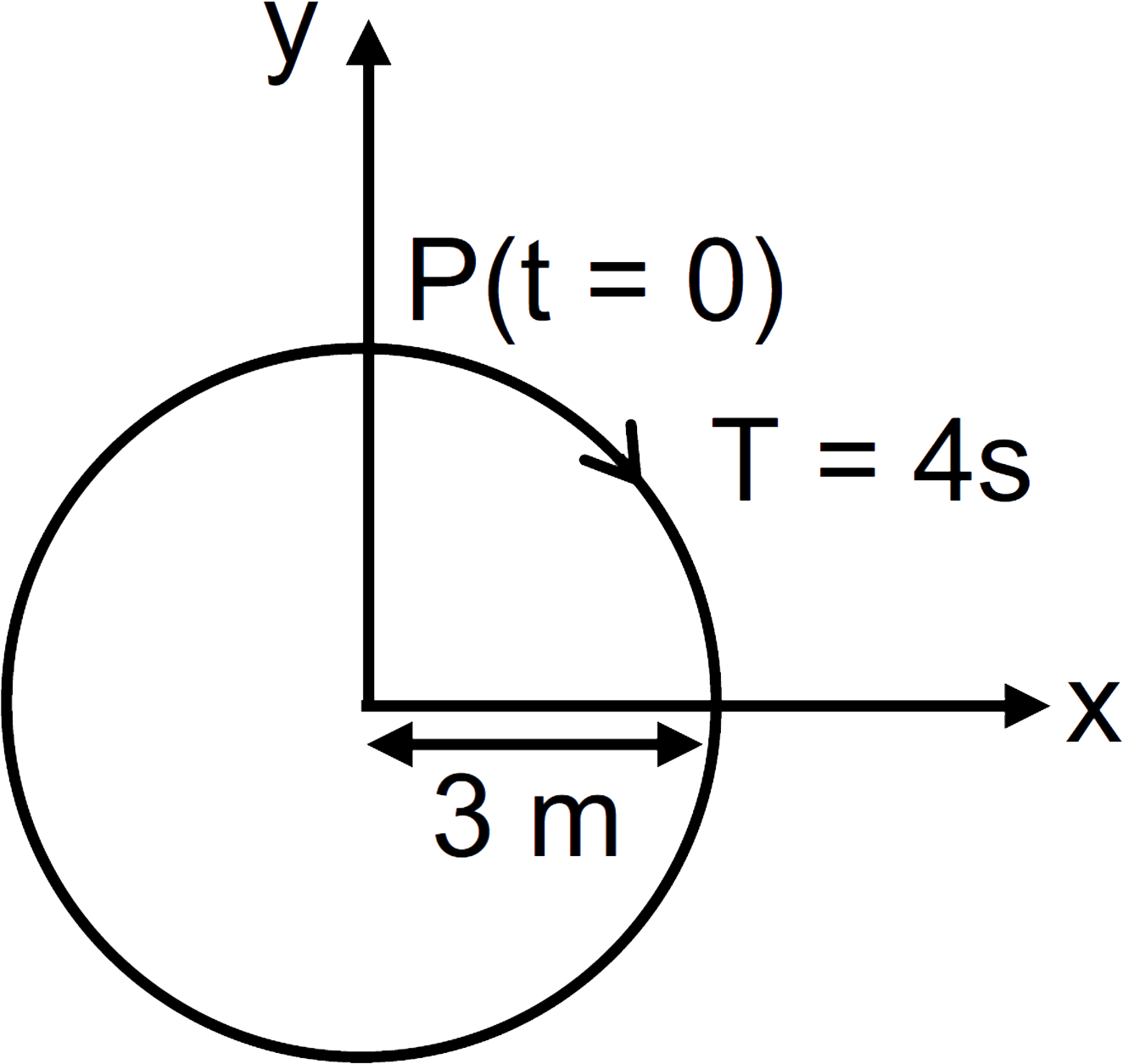
y-projection of the radius vector of rotating particle P is :
View SolutionThe displacement of a particle in simple harmonic motion in one time period is
View SolutionThe distance moved by a particle in simple harmonic motion in one time period is
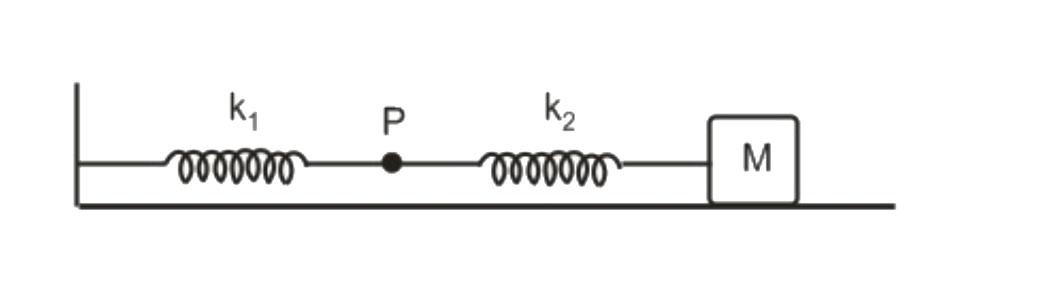
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
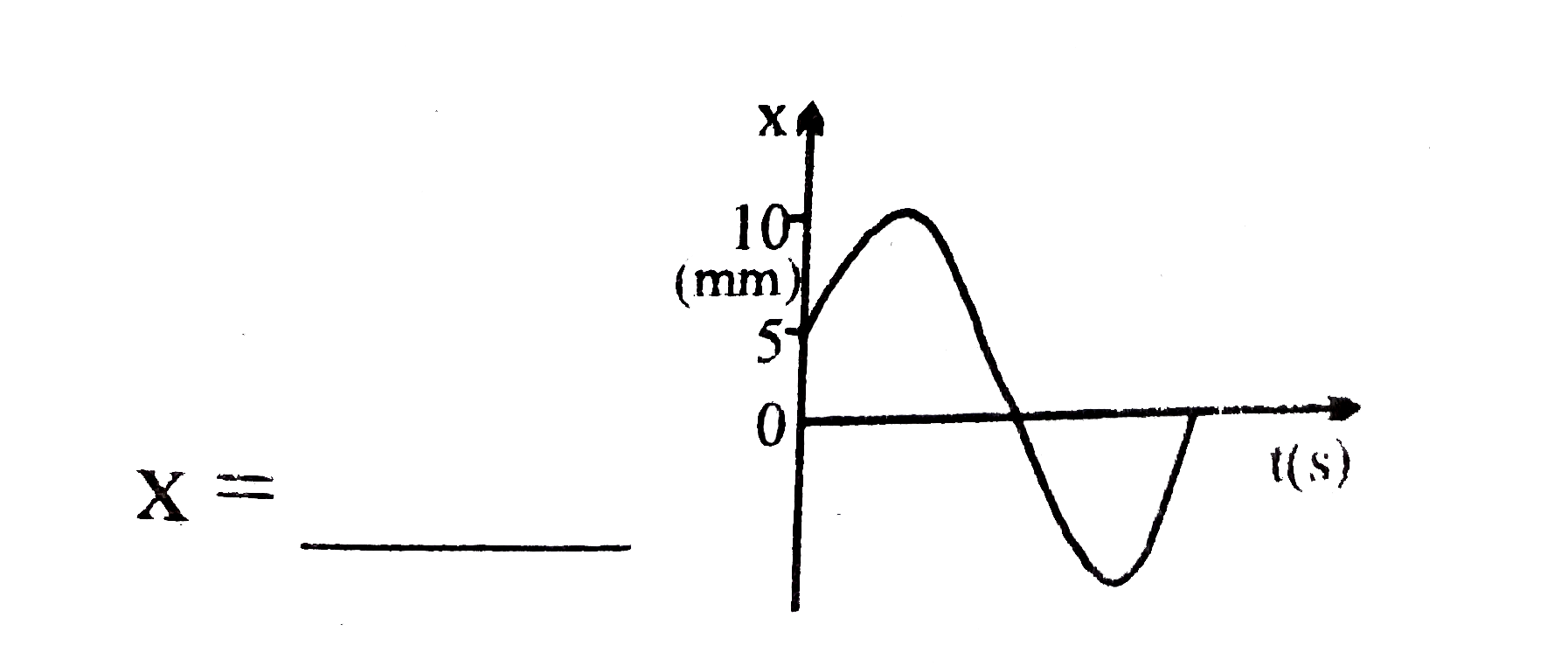
View Solution
