The radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.

y-projection of the radius vector of rotating particle P is :
y(t)=3cos(πt2), where y in m
y(t)=−3cos2πt, where y in m
y(t)=4sin(πt2), where y in m
y(t)=3cos(3πt2), where y in m
The correct Answer is:A
T=2πω=4,ω=π2
y co-ordinate starts from maximum
So y=Acos(ωt)
Y=3cos(π2t)
Similar Questions
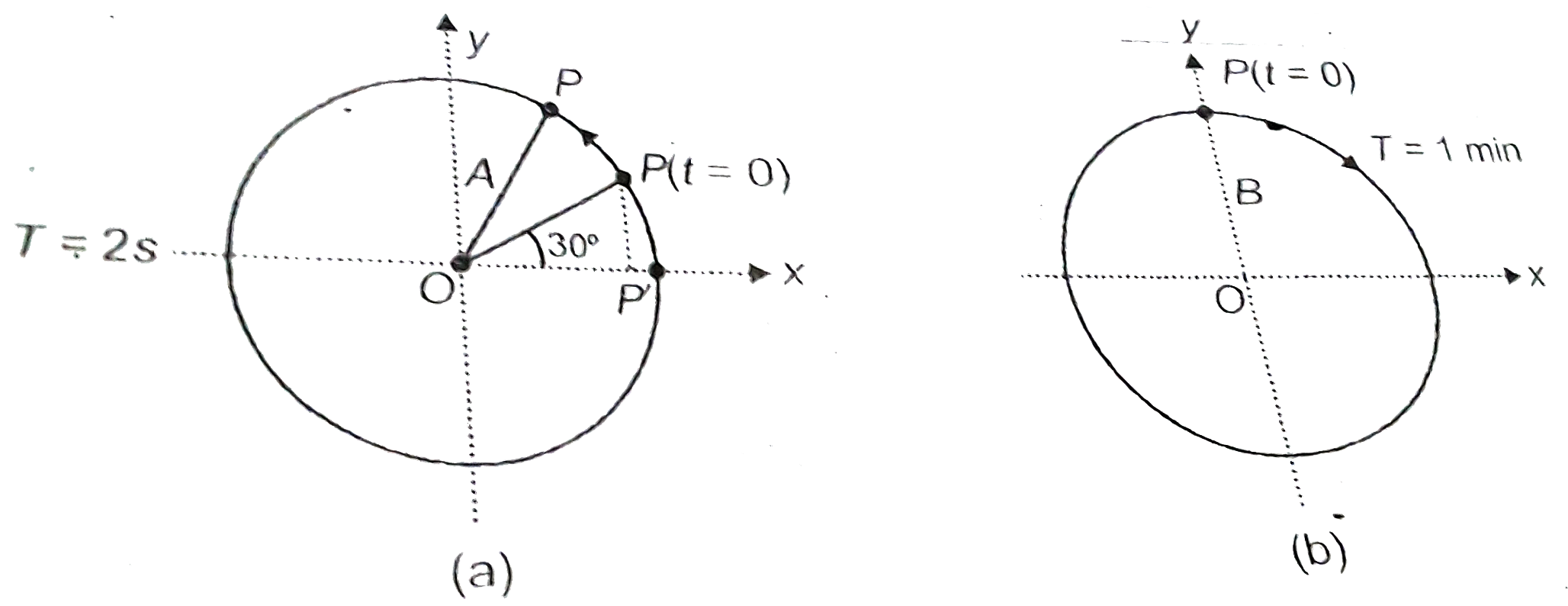
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
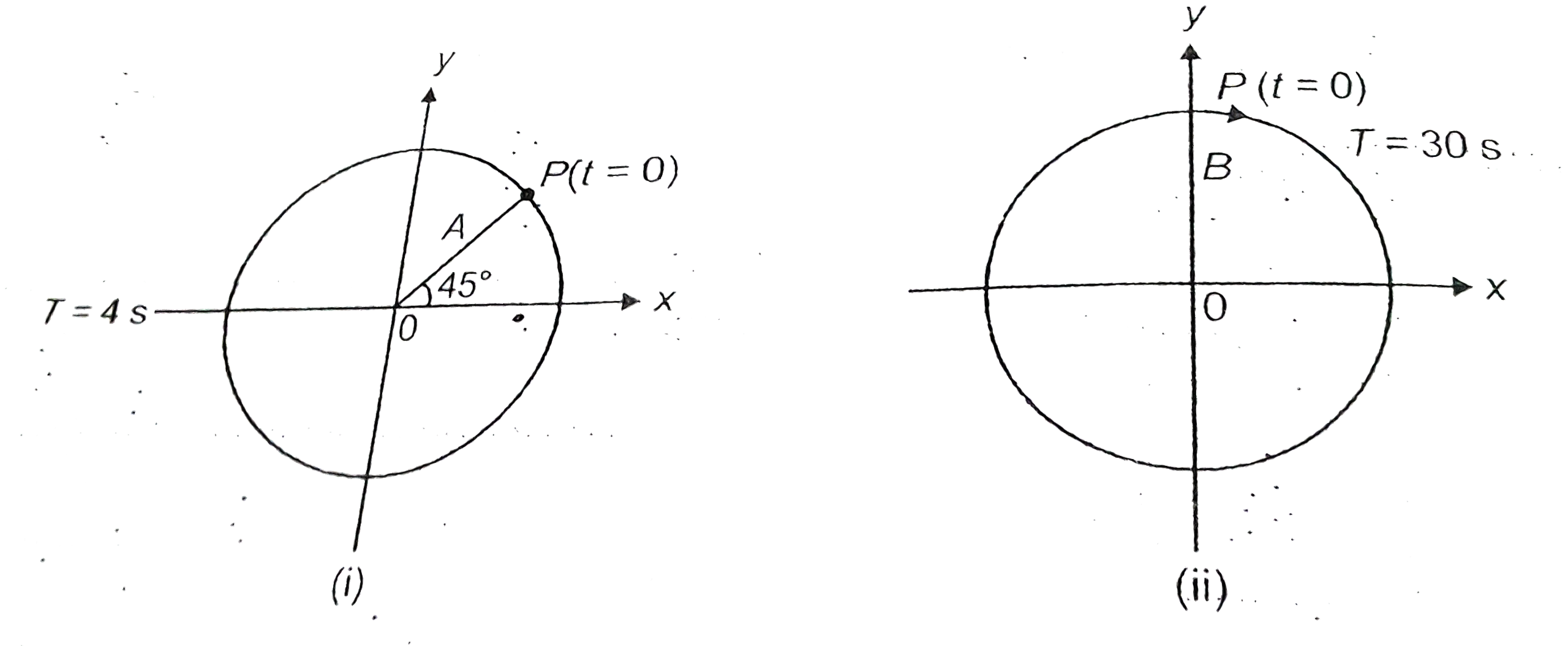
View SolutionThe following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
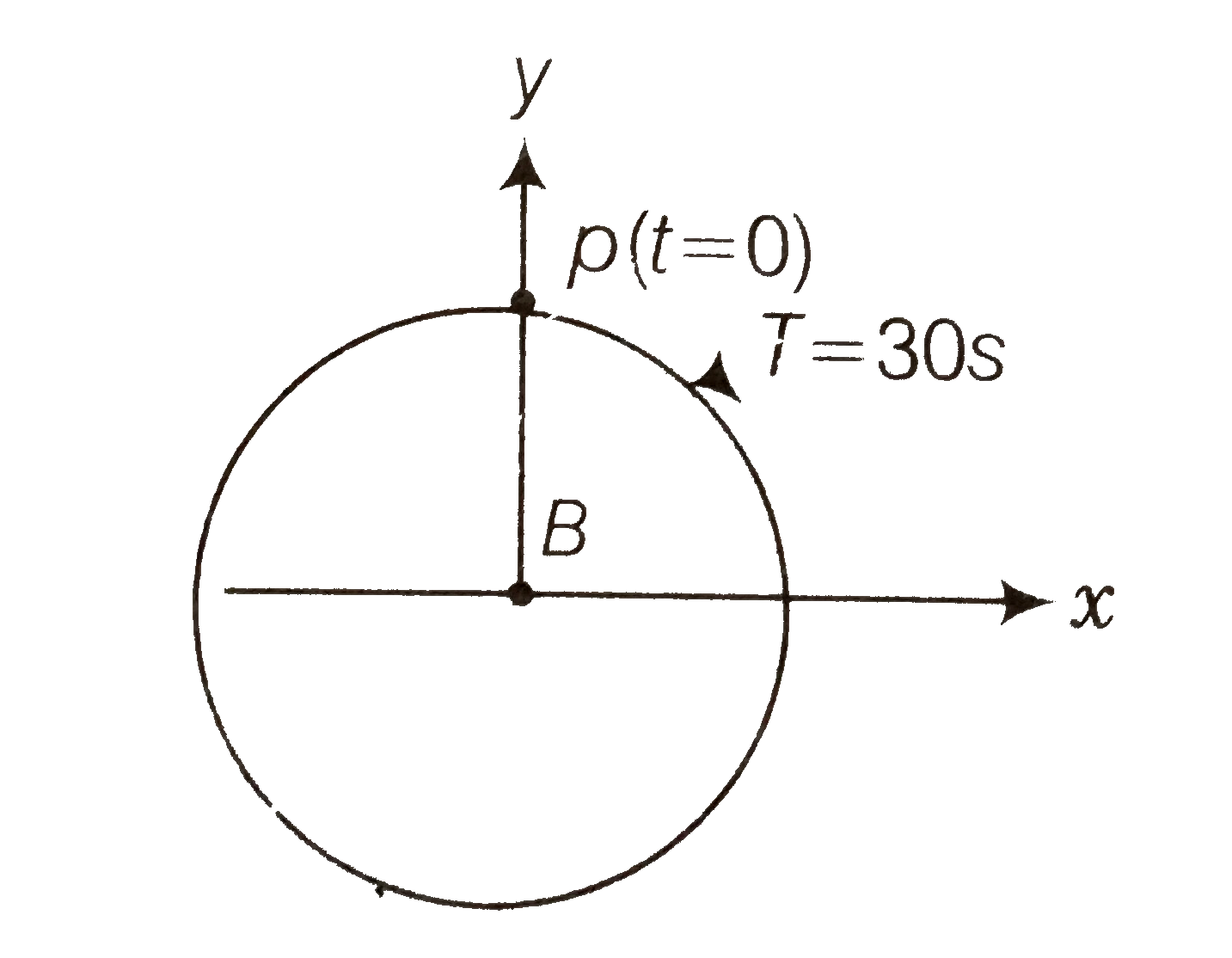
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
View Solution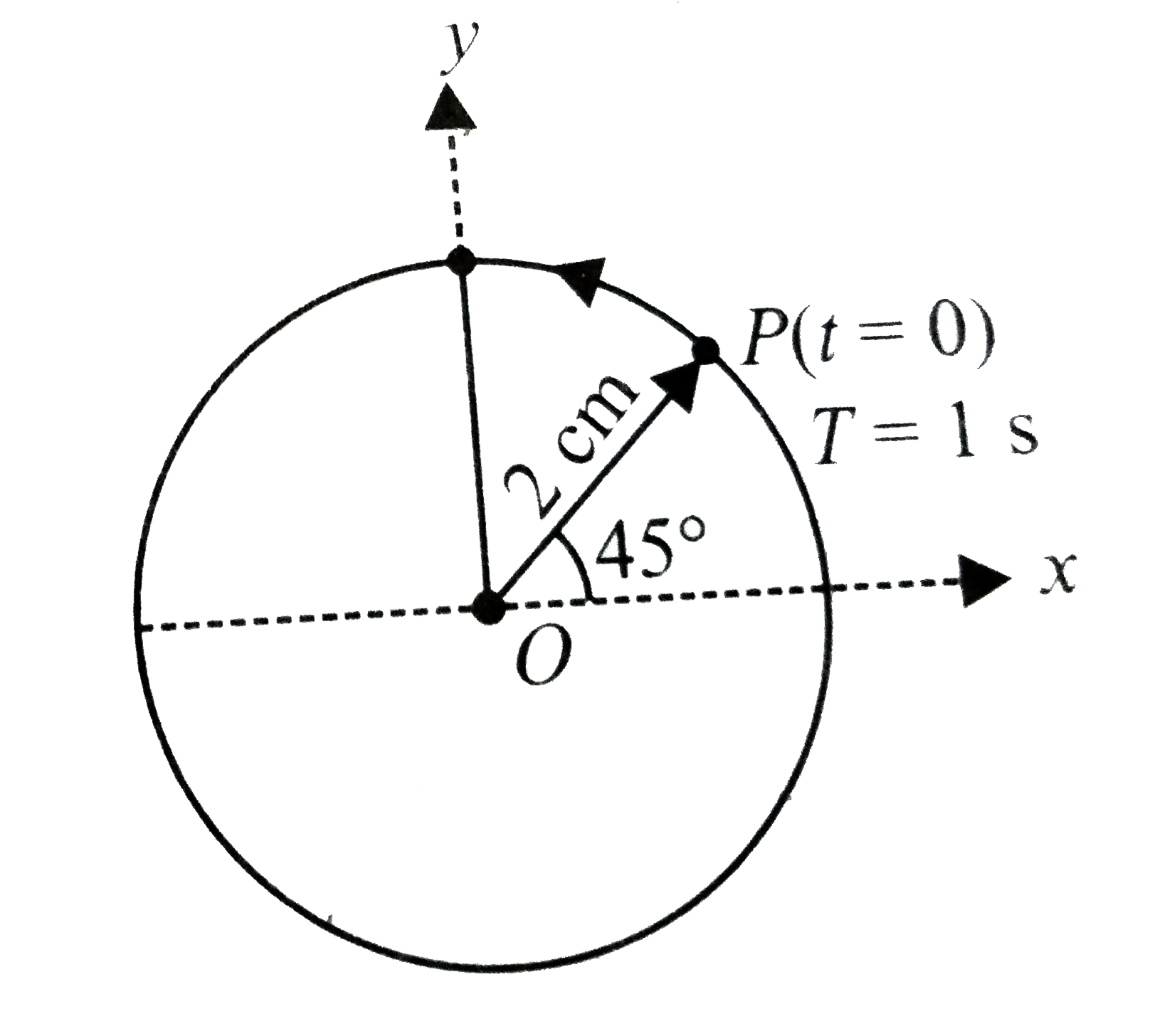
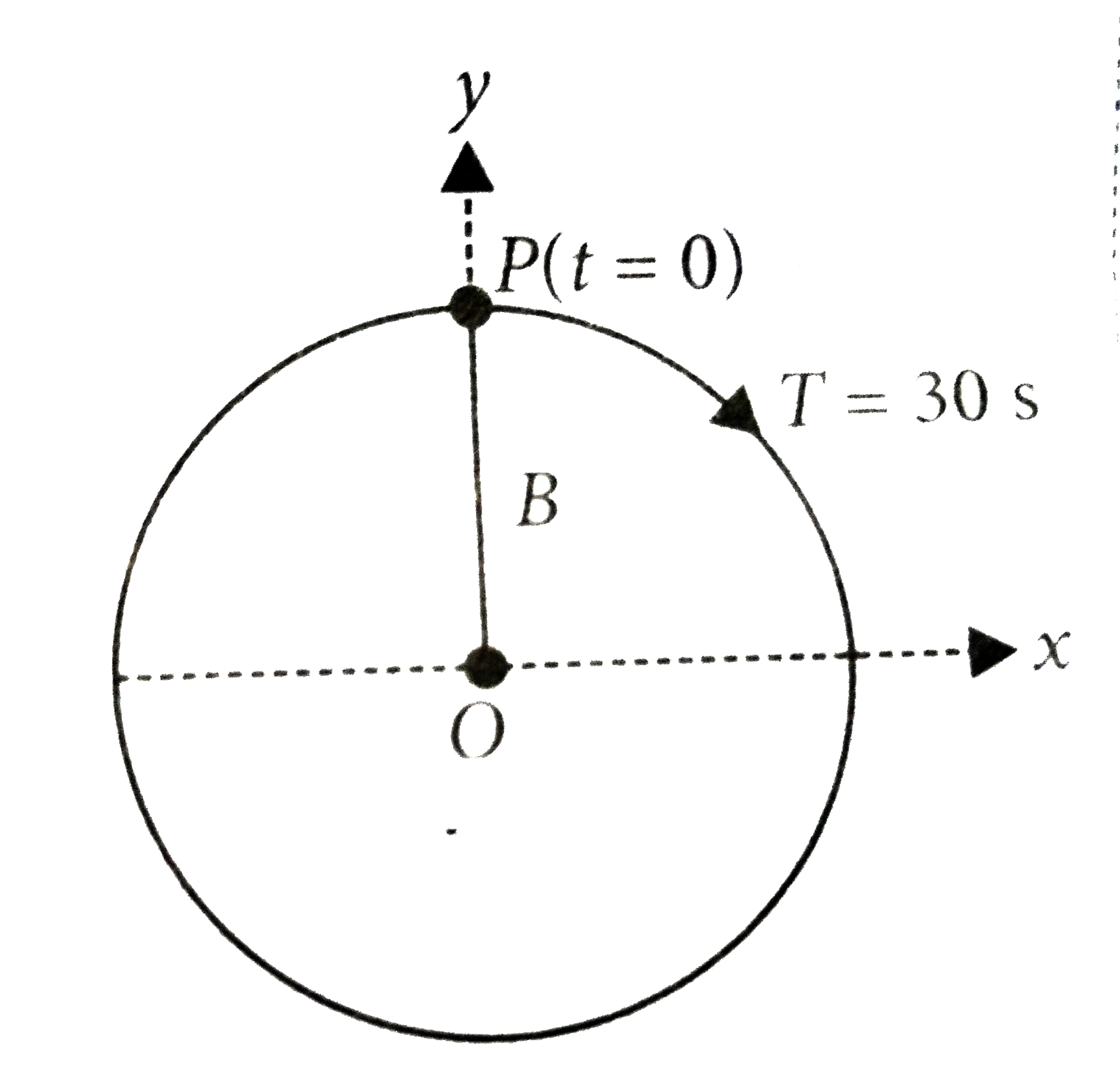
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
View SolutionThe period of revolution of a satellite in an orbit of radius 2R is T. What will be its period of revolution in an orbit of radius 8R ?
View SolutionFor a satellite orbiting close to the surface of earth the period of revolution is 84min. The time period of another satellite orbiting at a height three times the radius of earth from its surface will be
View SolutionIf T be the period of revolution of a plant revolving around sun in an orbit of mean radius R, then identify the incorrect graph.
View SolutionFind the period of revolution of a satellite revolving the earth at a height of 200km above earth's surface ? Radius of earth = 6400 km
View SolutionAssertion (A) : The time period of revolution of a satellite around a planet is directly proportional to the radius of the orbit of the satellite.
Reason (R) : Artifical satellite do not follow Kepler's laws of planatory motion.
View Solution
